练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知在△ABC中，AB=AC=10cm，高AD=8cm，求：
    （1）BC的长；
    （2）△ABC的面积．
    考点：勾股定理
    专题：
    分析：（1）根据等腰三角形的性质得出BC=2BD，再根据勾股定理求出BD的长，进而得出结论；
    （2）直接根据三角形的面积公式求解．
    解答：解：（1）如图所示；
    ∵在△ABC中，AB=AC=10cm，高AD=8cm，
    ∴BC=2BD，BD=
    		AB2-BD2
    =
    		102-82
    =6cm，
    ∴BC=2×6=12cm；

    （2）∵BC=12cm，AD=8cm，
    ∴S△ABC=
    1
    2
    BC•AD=
    1
    2
    ×12×8=48cm2．
    点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

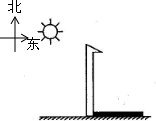    如图是王老师出示的他昨天画的一幅写生画，四个同学猜测他画这幅画的时间．请根据王老师给出的方向坐标，判断说的时间比较接近的是（　　）
    A、小丽说：“早上8时”
    B、小强说：“中午12时”
    C、小刚说：“下午5时”
    D、小明说：“哪个时间段都行”

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知x、y是有理数，且|3x-4|+（5y+7）2=0，求x2+y2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

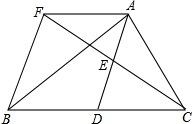    如图，在△ABC中，D是BC边的中点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，连接BF．
    （1）求证：四边形AFBD是平行四边形；
    （2）要使四边形AFBD是菱形，△ABC应满足什么条件？并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

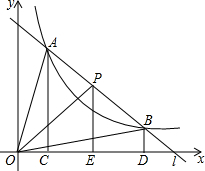    已知直线和双曲线交于A、B两点，P是线段AB上一点（P不与A、B重合），过点A、P、B分别向横坐标轴做垂线，垂足为C、D、E，连接OA、OB、OP，求证：S△POE＞S△AOC=S△BOD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

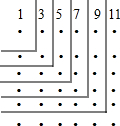    数形结合是一种重要的数学思想，认真观察图形，然后完成下列问题：
    （1）计算：1+3+5+7+9=
     
    2；
    （2）计算：1+3+5+7+9+11=
     
    2；
    （3）根据你发现的规律及图中的信息，请你类似（1）（2），用等式表示从1开始的n个连续奇数之和的结果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

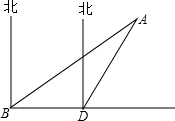    天然气管道铺设工程从B向正东方向进行，如图所示，从B处测得A点位于B点北偏东60°，从B向东前进400m到达D点，在D点测得A点位于北偏东45°方向，以A点为中心，半径为500m的圆形区域为居民住宅区，请计算后回答：天然气管道铺设工程是否会穿过居民住宅区？（
    		3
    ≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在△ABC中，∠1=∠2，∠3=∠4，请判断△ABC的形状．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

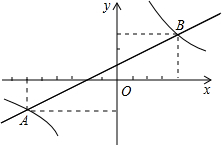    如图，一次函数y=kx+b的图象与反比例函数y=
    m
    x
    的图象相交于A、B两点．
    （1）根据图象，分别写出A、B的坐标；
    （2）求一次函数y=kx+b解析式；
    （3）求三角形AOB的面积．

    查看答案和解析>>

    同步练习册答案