
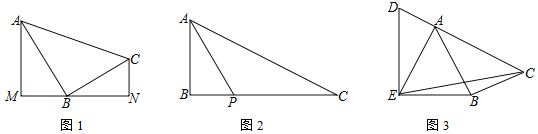
【题目】在△ABC中,∠ABC=90°.
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC=![]() ,求tanC的值;
,求tanC的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=![]() ,
,![]() ,直接写出tan∠CEB的值.
,直接写出tan∠CEB的值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)利用同角的余角相等判断出∠BAM=∠CBN,即可得出结论;
(2)如图,过点P作PF⊥AP交AC于F,先判断出△ABP∽△PQF,得出![]() ,再判断出△ABP∽△CQF,得出CQ=2a,进而建立方程用b表示出a,即可得出结论;
,再判断出△ABP∽△CQF,得出CQ=2a,进而建立方程用b表示出a,即可得出结论;
(3)先判断出![]() ,再同(2)的方法,即可得出结论.
,再同(2)的方法,即可得出结论.
(1)∵AM⊥MN,CN⊥MN,
∴∠AMB=∠BNC=90°,
∴∠BAM+∠ABM=90°,
∵∠ABC=90°,
∴∠ABM+∠CBN=90°,
∴∠BAM=∠CBN,
∵∠AMB=∠NBC,
∴△ABM∽△BCN;
(2)如图,过点P作PF⊥AP交AC于F,
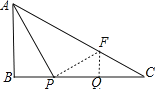
在Rt△AFP中,tan∠PAC=![]() ,
,
同(1)的方法得,△ABP∽△PQF,
∴![]() ,
,
设AB=![]() a,PQ=2a,BP=
a,PQ=2a,BP=![]() b,FQ=2b(a>0,b>0),
b,FQ=2b(a>0,b>0),
∵∠BAP=∠C,∠B=∠CQF=90°,
∴△ABP∽△CQF,
∴![]() ,∴CQ=
,∴CQ=![]() =2a,
=2a,
∵BC=BP+PQ+CQ=![]() b+2a+2a=4a+
b+2a+2a=4a+![]() b,
b,
∵∠BAP=∠C,∠B=∠B=90°,
∴△ABP∽△CBA,
∴![]() ,
,
∴BC=![]() ,
,
∴4a+![]() b=
b=![]() ,
,
∴a=![]() b,
b,
∴BC=4×![]() b+
b+![]() b=
b=![]() b,AB=
b,AB=![]() a=b,
a=b,
在Rt△ABC中,tanC=![]() ;
;
(3)在Rt△ABC中,sin∠BAC=![]() ,
,
如图,过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于H,
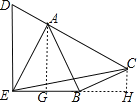
∵∠DEB=90°,
∴CH∥AG∥DE,
∴![]() ,
,
同(1)的方法得,△ABG∽△BCH,
∴![]() =
=![]() ,
,
设BG=4m,CH=3m,AG=4n,BH=3n,
∵AB=AE,AG⊥BE,
∴EG=BG=4m,
∴GH=BG+BH=4m+3n,
∴![]() ,
,
∴n=2m,
∴EH=EG+GH=4m+4m+3n=8m+3n=8m+6m=14m,
在Rt△CEH中,tan∠BEC=![]() .
.


科目:初中数学 来源: 题型:
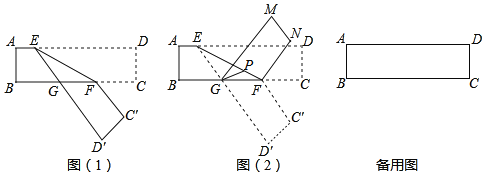
【题目】如图为长方形纸带,AD平行BC,E、F分别是边AD、BC上一点,∠DEF=α,α为锐角且α≠60°,将纸带沿EF折叠如图(1),再由GF折叠如图(2),若GP平分∠MGF交直线EF于点P,则∠GPE=_____(含α的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个边长为1的正方形纸片分割成7个部分,第①部分是边长不1的正方形纸片面积的一半,第②部分是第①部分面积的半,第③部分是第③部分面积的一半,…,依次类推.
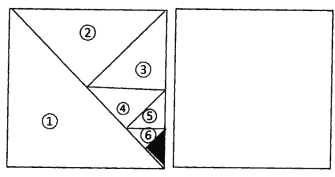
(1)阴影部分的面积是多少?
(2)受此启发,你能求出![]() 的值吗?
的值吗?
(3)请你利用图中右侧的正方形,再设计能求![]() 的值的几何图形.(只画出图形即可)
的值的几何图形.(只画出图形即可)
(4)根据以上规律,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,AD∥BC,要判别四边形ABCD是平行四边形,还需满足条件( )
A. ∠A+∠C=180°B. ∠B+∠D=180°
C. ∠A+∠B=180°D. ∠A+∠D=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2,x3,x2019都是不等于0的有理数,若![]() ,求y1的值.
,求y1的值.
当x1>0时,![]() ;当x1<0时,
;当x1<0时,![]() ,所以y1=±1,值有两个.
,所以y1=±1,值有两个.
(1)若![]() ,求y2的值为 ;
,求y2的值为 ;
(2)若![]() ,则y3的值为 ;
,则y3的值为 ;
(3)由以上探究猜想,![]() 共有 个不同的值,在y2019这些不同的值中,最大的值和最小的值的差等于 .
共有 个不同的值,在y2019这些不同的值中,最大的值和最小的值的差等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
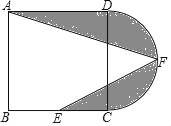
A. 18+36π B. 24+18π C. 18+18π D. 12+18π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数![]() 的大致图象;
的大致图象;
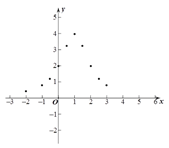
(4)结合函数图象,请写出函数![]() 的一条性质:______________________.
的一条性质:______________________.
(5)解决问题:如果函数![]() 与直线y=a的交点有2个,那么a的取值范围是______________ .
与直线y=a的交点有2个,那么a的取值范围是______________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com