
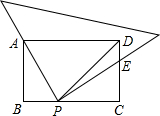
 长方形ABCD中,DP平分∠ADC交BC于P点,将一个直角三角板的直角顶点放在P点处,并使它的一条直角边过A点,另一条直角边交CD于E点.
长方形ABCD中,DP平分∠ADC交BC于P点,将一个直角三角板的直角顶点放在P点处,并使它的一条直角边过A点,另一条直角边交CD于E点.| 1 |
| 3 |
| 2 |
| 3 |
|
 ∵△PAB≌△EPC,
∵△PAB≌△EPC,| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 18 |
| 5 |
| 18 |
| 5 |
| 12 |
| 5 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 9 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 12 |
| 5 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
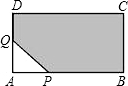 如图,在长方形ABCD中AB=12cm,AD=8cm,点P,Q都从点A出发,分别沿AB和AD运动,且保持AP=AQ,在这个变化过程中,图中的阴影部分的面积也随之变化.当AP由2cm变到8cm时,图中阴影部分的面积是增加了,还是减少了?增加或减少了多少平方厘米?
如图,在长方形ABCD中AB=12cm,AD=8cm,点P,Q都从点A出发,分别沿AB和AD运动,且保持AP=AQ,在这个变化过程中,图中的阴影部分的面积也随之变化.当AP由2cm变到8cm时,图中阴影部分的面积是增加了,还是减少了?增加或减少了多少平方厘米?查看答案和解析>>
科目:初中数学 来源: 题型:
 ;
;| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com