
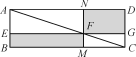
【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
(以上材料来源于《古证复原的原则》《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据上图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),
S矩形EBMF=S△ABC-(______________+______________).
易知,S△ADC=S△ABC,______________=______________,______________=______________.
可得S矩形NFGD=S矩形EBMF.
科目:初中数学 来源: 题型:
【题目】七个边长为1的正方形按如图所示的方式放置在平面直角坐标系中,直线l经过点A(4,4)和点B,且将这七个正方形的面积分成相等的两部分,则直线l的函数表达式是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答下列问题:
神奇的等式
当a≠b时,一般来说会有a2+b≠a+b2,然而当a和b是特殊的分数时,这个等式却是成立的例如:
(![]() )2+
)2+![]() =
=![]() +
+![]() ,(
,(![]() )2+
)2+![]() =
=![]() +
+![]() ,(
,(![]() )2+
)2+![]() =
=![]() +(
+(![]() )2,…(
)2,…(![]() )2+
)2+![]() =
=![]() +(
+(![]() )2,…
)2,…
(1)特例验证:
请再写出一个具有上述特征的等式: ;
(2)猜想结论:
用n(n为正整数)表示分数的分母,上述等式可表示为: ;
(3)证明推广:
①(2)中得到的等式一定成立吗?若成立,请证明;若不成立,说明理由;
②等式(![]() )2+
)2+![]() =
=![]() +(
+(![]() )2(m,n为任意实数,且n≠0)成立吗?若成立,请写出一个这种形式的等式(要求m,n中至少有一个为无理数);若不成立,说明理由.
)2(m,n为任意实数,且n≠0)成立吗?若成立,请写出一个这种形式的等式(要求m,n中至少有一个为无理数);若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
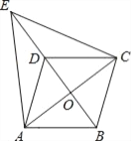
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若AC=8,AB=5,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
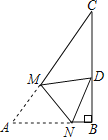
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=![]() ,tanB=
,tanB=![]() .半径为2的⊙C, 分别交AC、BC于点D、E,得到
.半径为2的⊙C, 分别交AC、BC于点D、E,得到![]() .
.
(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,BD=CE,将线段AE沿AC翻折,得到线段AM,连结EM交AC于点N,连结DM、CM.以下说法:①AD=AM,②DE=ME,③CN=![]() EC,④S△ABD=S△ACM中,正确的是_____.
EC,④S△ABD=S△ACM中,正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中, AB=11 , AC= 5 ,∠ BAC 的平分线 AD 与边 BC 的垂直平分线 DG 相 交于点 D ,过点 D 分别作 DE⊥AB ,DF⊥AC ,垂足分别为 E 、F,求BE的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com