
分析 (1)先把二次根式化为最简二次根式,然后合并即可;
(2)先把二次根式化为最简二次根式,然后合并即可;
(3)利用二次根式的除法法则运算.
解答 解:(1)原式=2$\sqrt{6}$-$\frac{\sqrt{6}}{3}$-$\frac{\sqrt{30}}{2}$-$\sqrt{5}$
=$\frac{5\sqrt{6}}{3}$-$\frac{\sqrt{30}}{2}$-$\sqrt{5}$;
(2)原式=2($\sqrt{2}$+1)+3$\sqrt{2}$-2$\sqrt{2}$
=2$\sqrt{2}$+2+$\sqrt{2}$
=3$\sqrt{2}$+2;
(3)原式=5$\sqrt{48÷3}$-6$\sqrt{27÷3}$+4$\sqrt{15÷3}$
=20-18+4$\sqrt{5}$
=2+4$\sqrt{5}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
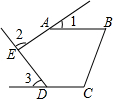 如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,若∠1=32°,∠3=60°,则∠2等于( )
如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,若∠1=32°,∠3=60°,则∠2等于( )| A. | 92° | B. | 88° | C. | 98° | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了丰富少年儿童的业余生活,某社区要在如下图的AB上建一座图书室P.本社区有两所学校,所在的位置为点C和点D处,CA⊥AB于点A,DB⊥AB于点B.已知AB=25km,DB=10km,CA=15km,要求图书室P到两所学校的距离相等.
为了丰富少年儿童的业余生活,某社区要在如下图的AB上建一座图书室P.本社区有两所学校,所在的位置为点C和点D处,CA⊥AB于点A,DB⊥AB于点B.已知AB=25km,DB=10km,CA=15km,要求图书室P到两所学校的距离相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com