
分析 (1)设出顶角的度数,然后表示出底角,列方程求解即可;
(2)已知给出的等腰三角形的一边长为5,但没有明确指明是底边还是腰,因此要分两种情况,分类讨论解答.
解答 解:(1)设顶角为x度,则底角为2x度,
则:x+2x+2x=180,
解得:x=36,
所以这个三角形三个内角的度数分别为36°、72°、72°;
(2)∵等腰三角形的一边长为5,周长为12,
∴当5为底时,其它两边都为3.5、3.5,5、3.5、3.5可以构成三角形;
当5为腰时,其它两边为5和2,5、5、2可以构成三角形.
∴另两边是3.5、3.5或5、2.
点评 本题考查了等腰三角形的性质及三角形三边关系;在解决与等腰三角形有关的问题,由于等腰所具有的特殊性质,很多题目在已知不明确的情况下,要进行分类讨论,才能正确解题,因此,解决和等腰三角形有关的边角问题时,要仔细认真,避免出错.同时考查了方程的思想.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{{2}^{4022}}$ | B. | $\frac{1}{{2}^{4024}}$ | C. | $\frac{1}{{2}^{4026}}$ | D. | $\frac{1}{{2}^{4028}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,点A和点B分别在x轴的正半轴和y轴的正半轴上,且OA=6,OB=8,点D是AB的中点.
在平面直角坐标系中,点A和点B分别在x轴的正半轴和y轴的正半轴上,且OA=6,OB=8,点D是AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
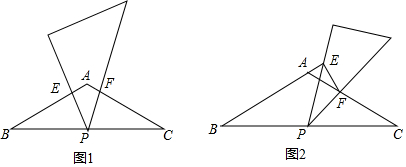
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com