
如图1,点A是线段BC上一点,△ABD和△ACE都是等边三角形.
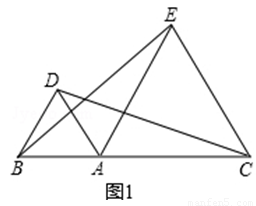
(1)连结BE,CD,求证:BE=CD;
(2)如图2,将△ABD绕点A顺时针旋转得到△AB′D′.
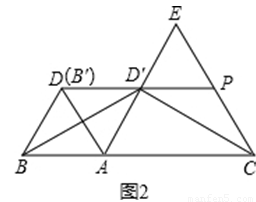
①当旋转角为多少度时,边AD′落在AE上;
②在①的条件下,延长DD’交CE于点P,连接BD′,CD′.当线段AB、AC满足什么数量关系时,BD′与CD′相等?并给予证明.
(1)详见解析;(2)①旋转角为60°;②当AC=2AB时,BD′=CD′,证明详见解析.
【解析】
试题分析:(1)容易证明⊿ABE≌⊿ADC,从而得证.(2)①由已知条件得∠BAD=60°,∠CAE=60°,所以∠DAE=60°,所以当AD′落在AE上时,旋转角为60°.②若BD′=CD′,则必有∠D′BC=∠D′CB,又因为AB=AD′,所以有∠ABD′=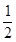 ∠EAC=30°,所以有∠ACD′=30°,从而发现AB=
∠EAC=30°,所以有∠ACD′=30°,从而发现AB=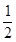 AC.证明的过程和上面分析的过程刚好相反,把AB=
AC.证明的过程和上面分析的过程刚好相反,把AB=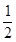 AC当作条件,利用等边三角形的性质以及旋转的性质即可证明.
AC当作条件,利用等边三角形的性质以及旋转的性质即可证明.
试题解析:(1)证明:∵△ABD和△ACE都是等边三角形.
∴AB=AD,AE=AC,∠BAD=∠CAE=60°,
∴∠BAD+∠DAE=∠CAE+∠DAE,
即∠BAE=∠DAC,
在△BAE和△DAC中,
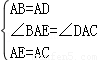 ,
,
∴△BAE≌△DAC(SAS),
∴BE=CD; 4分
(2)解:①∵∠BAD=∠CAE=60°,
∴∠DAE=180°﹣60°×2=60°,
∵边AD′落在AE上,
∴旋转角=∠DAE=60°; 7分
②当AC=2AB时,BD′=CD′.
理由如下:由旋转可知,AB′与AD重合,
∴AB=BD=DD′=AD′
∴四边形ABDD′是菱形,
∴∠ABD′=∠DBD′=∠ABD=×60°=30°
∵△ACE是等边三角形,
∴AC=AE,∠ACE=60°,
∵AC=2AB,
∴AE=2AD′,
∴∠PCD′=∠ACD′=∠ACE=×60°=30°,
∠ABD′=∠ACD′
∴BD′=CD′ 11分
考点:1、旋转的性质;2、等边三角形的性质;3、全等三角形的判定.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com