
| A. | 2 | B. | 8 | C. | 2或8 | D. | 8或16 |
分析 分两种情况:①若BC为等腰三角形的腰,即方程x2-5mx+4m2=0有一个根为8,将x=8代入方程求得m的值,再将m的值代回方程求得x的值,根据三角形三边之间的关系判断是否能构成三角形;②若BC为等腰三角形的底边,则方程x2-5mx+4m2=0有两个相等的实数根,根据判别式为0求得m的值,再判断即可得.
解答 解:根据题意,若BC为等腰三角形的腰,则方程x2-5mx+4m2=0有一个根为8,
将x=8代入得:64-40m+4m2=0,即m2-10m+16=0,
解得:m=2或m=8,
当m=2时,方程为x2-10x+16=0,解得:x=2或x=8,符合题意;
当m=8时,方程为x2-40x+256=0,解得:x=32或x=8,
此时8+8<32,不能构成三角形,舍去;
若BC为等腰三角形的底边,则方程x2-5mx+4m2=0有两个相等的实数根,
∴△=25m2-16m2=0,
解得:m=0,
此时方程为x2=0,得x=0,不符合题意,舍去;
综上m的值为2,
故选:A.
点评 本题主要考查根的判别式、方程的解的定义、等腰三角形的性质及三角形三边之间的关系,根据等腰三角形的性质分类讨论是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1004<a<1005 | B. | 1004≤a<1005 | ||
| C. | 1004<a<1005或-1005≤a<-1004 | D. | 1004≤a<1005或-1005<a≤-1004 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
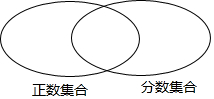 把下列各数填在相应的圆圈集合内:
把下列各数填在相应的圆圈集合内:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
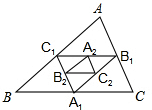 如图,在△ABC中,A1、B1、C1分别是BC、CA、AB的中点,A2、B2、C2分别是B1C1、C1A1、A1B1的中点,…,An、Bn、Cn分别是Bn-1Cn-1、Cn-1An-1、An-1Bn-1的中点,假设△ABC的周长为a,则△A1B1C1的周长为$\frac{1}{2}$a,△A2B2C2的周长为$\frac{1}{4}$a,…,△AnBnCn的周长为$\frac{1}{{2}^{n}}$a.
如图,在△ABC中,A1、B1、C1分别是BC、CA、AB的中点,A2、B2、C2分别是B1C1、C1A1、A1B1的中点,…,An、Bn、Cn分别是Bn-1Cn-1、Cn-1An-1、An-1Bn-1的中点,假设△ABC的周长为a,则△A1B1C1的周长为$\frac{1}{2}$a,△A2B2C2的周长为$\frac{1}{4}$a,…,△AnBnCn的周长为$\frac{1}{{2}^{n}}$a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正整数和正分数统称正有理数 | B. | 两个无理数相乘的结果可能等于零 | ||
| C. | 正整数,0,负整数统称为整数 | D. | 3.1415926是小数,也是分数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
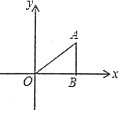 如图.在△ABO中,AB丄OB,OB=$\sqrt{3}$,AB=1,将△ABO绕O点逆时计旋转90°后得到△A1B1O,则点A1的坐标为( )
如图.在△ABO中,AB丄OB,OB=$\sqrt{3}$,AB=1,将△ABO绕O点逆时计旋转90°后得到△A1B1O,则点A1的坐标为( )| A. | (-1,$\sqrt{3}$) | B. | (-1,$\sqrt{3}$)或(1,-$\sqrt{3}$) | C. | (-1,-$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$)或(-$\sqrt{3}$,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com