
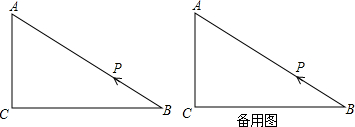
ñøö— È´1Èˋ¡ªƒïÀüC=90ÀÐȘAC=6cmȘBC=8cmȘçû°—ABçá°ÊȘ§½Ñ½çû°—AP=AB-tÈÛ
È´2ÈˋñøAC=APȘCP=APê§øøúÕ¢—§ãÇޥǢèÈ£
È´3Èˋ¿»çÐPæ¼PMÀëACÆÖMȘ¡ªƒïêãÅöçáÅåøòçûPQ=PAȘå·çû°—t¥Ç¢èÈÛ
§ãÇÞ §ãȤȴ1ÈˋÀÔÀüC=90ÀÐȘAC=6cmȘBC=8cmȘ
ÀÁAB=$\sqrt{{6}^{2}+{8}^{2}}=10$cmȘ
ÀÁAP=AB-t=10-2tȘ
¿òÇÞ¯¡öˆÈ¤10-2tÈ£
È´2ÈˋçÝÀ¼ACPöˆçàî■໧úÅöȘAC=AP=6Ș
ÀÁPB=AB-APȘ
¢èçûȤ2t=10-6=4È£
§ãçûȤt=2È£
çÝÀ¼ACPöˆçàî■໧úÅöȘCP=APȘ
ÀÁBP=AB-AP=CP=5Ș
ÀÁ2t=5È£
§ãçûȤt=2.5È£
ÇÞȤçÐP°—ñÂ2£·2.5ûŠÈ˜À¼ACPöˆçàî■໧úÅöÈ£
È´3ÈˋçÝt=$\frac{60}{17}$òÝȘùáÝÔÅöPQPÀðAòúêãÅöȘ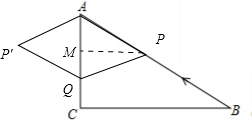
àÓ륿»çÐPæ¼PMÀëACÆÖMȘ
ÀÔAQ=tȘÆèÈ´2Èˋ¢èøˆÈ˜AM=$\frac{1}{2}$AQ=$\frac{1}{2}$tcmȘ
ÀÁAP=PQȘAP=10-2tȘ
$\frac{\frac{1}{2}t}{10-2t}=\frac{6}{10}$Ș
§ãçûȤt=$\frac{60}{17}$Ș
çÝt=$\frac{60}{17}$òÝȘùáÝÔÅöPQPÀðAòúêãÅöÈÛ
çÐóâ Çùäãø¼Øˆ¢¥ýÕêùùáÝÔÅöæܤüäãȘ¿Ä¥■òú¡ªƒï¿Ç¿èÑ´âÚÀÂêãÅöçáÅåøòçàøˆòÑçЧãÇÞȘòúøÅ¢¥î¿øÃäãȘáîÑàó¨ÇµÈ˜í»àñâ«ÆûêãÅöçáéÅÑ´§½ÅŧãÇÞòú§ãäã¿Ä¥■ÈÛ



| áõ¥Ñ | ¡ÔøÅ¢ö°ä | áõ¥Ñ | °¾øÅ¢ö°ä |
| ¡ÔØ£ | ¡ÔØ£ûãñî¢ö°äëó¥—ÈÀ | °¾Ø£ | °¾Ø£ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôѱ | ¡Ôѱûãñî¢ö°äëó¥—ÈÀ | °¾Ñ± | °¾Ñ±ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôà» | ¡Ôà»ûãñî¢ö°äëó¥—ÈÀ | °¾à» | °¾à»ûãñî¢ö°äëó¥—ÈÀ |
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤîÀåþäã
| AÈÛ |  | BÈÛ |  | CÈÛ |  | DÈÛ |  |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ䟢íäã
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ§ãÇÞäã

ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤîÀåþäã
| AÈÛ | 4 | BÈÛ | 3 | CÈÛ | 1 | DÈÛ | 0 |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ§ãÇÞäã
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ§ãÇÞäã
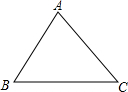 åÖàÓë¥ùªòƒçáÀ¼ABCøÅÈÛ
åÖàÓë¥ùªòƒçáÀ¼ABCøÅÈÛýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤîÀåþäã
| AÈÛ | 2x4 | BÈÛ | 2x3 | CÈÛ | 3x4 | DÈÛ | 3x3 |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¯ìÑàøôÅé - êñü¯ýÃêÅÝÚ - òåäãêÅÝÚ
¤±ÝÝòÀ£Ëêˆë½öËñ´¤ëý£ê¥ÅéüƒìÝ´ó§ä´ | ë½èüÆŤÎÅéüƒìÝ´æ´ú½ | çÓÅéíˋóÙƒìÝ´æ´ú½ | èÌâºòñÅÕößø¼ØÍÆŤÎÅéüƒìÝ´æ´ú½ | èÌóµúøà´ƒìÝ´æ´ú½
öËñ´¤ëý£ê¥ÅéüƒìÝ´çÓ£¯È¤027-86699610 ƒìÝ´ÆòüðȤ58377363@163.com