练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情


    解：（1）∵  30 000÷5 000＝6,     ∴  能租出24间.              

    （2）设每间商铺的年租金增加x万元,则

        （30－）×（10＋x）－（30－）×1－×0.5＝275，    

            2 x 2－11x＋5＝0，   ∴ x＝5或0.5，                      

    ∴ 每间商铺的年租金定为10.5万元或15万元.                          

    （3）275万元不是最大年收益                      

         当每间商铺的年租金定为12.5万元或13万元.    

         达到最大年收益，最大是285万元              


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


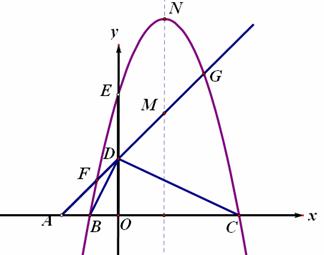
    如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，B为线段OA的中点，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M，点P为线段FG上一个动点(与F、G不重合)，PQ∥y轴与抛物线交于点Q。

      (1)求经过B、E、C三点的抛物线的解析式；

      (2)判断⊿BDC的形状，并给出证明；当P在什么位置时，以P、O、C为顶点的三角形是等腰三角形，并求出此时点P的坐标；

      (3)若抛物线的顶点为N，连接QN，探究四边形PMNQ的形状：①能否成为菱形；②能否成为等腰梯形？若能，请直接写出点P的坐标；若不能，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小明打算用一张半圆形的纸做一个圆锥。在制作过程中，他先将半圆剪成面积比为1:2的两个扇形．

    （1）请你在图中画出他的裁剪痕迹．（要求尺规作图，保留作图痕迹）

    （2）若半圆半径是3，大扇形作为圆锥的侧面，则小明必须在小扇形纸片中剪下多大的圆才能组成圆锥？小扇形纸片够大吗（不考虑损耗及接缝）？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     函数的自变量取值范围是         ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，点A，B，C，P的坐标分别为(0，2)，(3，2)，(2，3)，(1，1)．

        (1)请在图中画出△A′B′C′，使得△A′B′C′与△ABC关于点P成中心对称；

        (2)若一个二次函数的图像经过(1)中△A′B′C′的三个顶点，求此二次函数的关系式；

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某住宅小区六月份1日至6日每天用水量变化情况如折线图所示，那么这6天的平均用水量是(    )  

    A．30吨         B． 31 吨       C．32吨         D．33吨

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    因式分解=               .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，与左边正方形图案属于全等的图案是（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


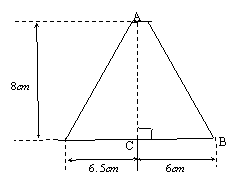
    将军家俱市场现有大批如图所示的边角余料

    (单位：cm)城西中学数学兴趣小组决定将其加工成等腰三角形，

    且方案如下：

    （1）三角形中至少有一边长为10 cm；

    （2）三角形中至少有一边上的高为8 cm

    请在备用图上画出出分割线，并求出相应图形面积

     


    查看答案和解析>>

    同步练习册答案