
分析 利用因式分解法解x2-7x+10=0得到x1=2,x2=5,然后根据三角形三边的关系和等腰三角形的性质得到三角形三边的关系得到腰为5,底边为2,再利用勾股定理求得高,进一步求得三角形的面积即可.
解答 解:x2-7x+10=0,
(x-2)(x-5)=0,
x-2=0或x-5=0,
解得:x1=2,x2=5,
当2为等腰三角形的腰时,5为底边,此时构不成三角形;
当5为等腰三角形的腰时,2为底边,此时三角形高为$\sqrt{{5}^{2}-{1}^{2}}$=2$\sqrt{6}$,
所以这个三角形的面积为$\frac{1}{2}$×2×2$\sqrt{6}$=2$\sqrt{6}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解.以及等腰三角形的性质与三角形的面积.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
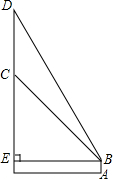 如图,在一座楼房墙上有一面广告牌,小明站在楼房正面距离该楼房12米的A处,自B点看正前方的广告牌上端D处的仰角为60°,下端C处的仰角为45°.求该广告牌上下两端之间的距离CD.(结果精确到0.1米)
如图,在一座楼房墙上有一面广告牌,小明站在楼房正面距离该楼房12米的A处,自B点看正前方的广告牌上端D处的仰角为60°,下端C处的仰角为45°.求该广告牌上下两端之间的距离CD.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
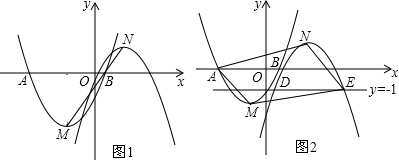
 今年夏天我市出现厄尔尼诺现象极端天气,多地引发滑坡、山洪等严重自然灾害.如图所示,ON为水平线,斜坡MN的坡比为1:$\sqrt{3}$,斜坡上一棵大树树干AB(树干AB垂直于底面ON)被大风刮倾斜15°后折断倒在山坡上,树的顶部恰好接触到坡面,经测量,大树被折断部分与坡面所成的角∠ADC=30°,AD=8米,∠BAC=15°.
今年夏天我市出现厄尔尼诺现象极端天气,多地引发滑坡、山洪等严重自然灾害.如图所示,ON为水平线,斜坡MN的坡比为1:$\sqrt{3}$,斜坡上一棵大树树干AB(树干AB垂直于底面ON)被大风刮倾斜15°后折断倒在山坡上,树的顶部恰好接触到坡面,经测量,大树被折断部分与坡面所成的角∠ADC=30°,AD=8米,∠BAC=15°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com