
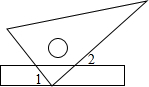
 小红把一把直尺与一块三角板如图放置,测得∠1=48°,则∠2的度数为( )
小红把一把直尺与一块三角板如图放置,测得∠1=48°,则∠2的度数为( )| A. | 38° | B. | 42° | C. | 48° | D. | 52° |
科目:初中数学 来源: 题型:选择题
 如图,△ABD≌△CDB,下面四个结论中不正确的是( )
如图,△ABD≌△CDB,下面四个结论中不正确的是( )| A. | △ABD和△CDB的面积相等 | B. | △ABD和△CDB的周长相等 | ||
| C. | ∠A+∠ABD=∠C+∠CBD | D. | AD∥BC,且AD=BC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
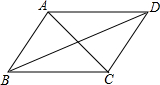 如图,下列条件不能够判定AB∥DC的是( )
如图,下列条件不能够判定AB∥DC的是( )| A. | ∠BAC=∠ACD | B. | ∠DCB+∠ABC=180° | C. | ∠ABD=∠BDC | D. | ∠DAC=∠BCA |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
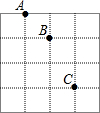 如图,利用平面直角坐标系画出的正方形网格中,若A(0,2),B(1,1),则点C的坐标为( )
如图,利用平面直角坐标系画出的正方形网格中,若A(0,2),B(1,1),则点C的坐标为( )| A. | (1,-2) | B. | (2,1) | C. | (1,-1) | D. | (2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
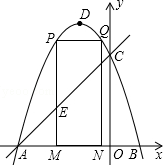 如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在一个装有2个红球和3个白球(每个球除颜色外都相同)的袋中任意摸出一球,摸到红球甲获胜,摸到白球乙获胜; | |
| B. | 从标有号数1到100的100张卡片中,随意抽取一张,抽到号数为奇数甲获胜,否则乙获胜; | |
| C. | 任意掷一枚质地均匀的骰子,掷出的点数小于4则甲获胜,掷出的点数大于4则乙获胜; | |
| D. | 让小球在如图所示的地板上自由地滚动,并随机地停在某块方块上,若小球停在黑色区域则甲获胜,若停在白色区域则乙获胜 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com