
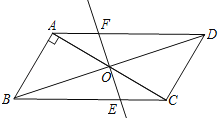
【题目】已知,如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=![]() ,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
(1)求证:当旋转角为90°时,四边形ABEF是平行四边形;
(2)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如能,说明理由并求出此时AC绕点O顺时针旋转的度数.
【答案】(1)见解析 (2)见解析
【解析】
(1)根据∠BAC=∠AOF=90°推出AB∥EF,根据平行四边形性质得出AF∥BE,即可推出四边形ABEF是平行四边形;
(2)证△DFO≌△BEO,推出OF=OE,得出四边形BEDF是平行四边形,根据勾股定理求出AC,求出OA=AB=1,求出∠AOB=45°,根据∠AOF=45°,推出EF⊥BD,根据菱形的判定推出即可.
(1)证明:∵∠AOF=90°,∠BAO=90°,
∴AB∥EF,
又∵平行四边形ABCD,
∴AF∥EB,
∴四边形ABEF是平行四边形;
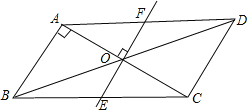
(2)当旋转角∠AOF=45°时,四边形BEDF是菱形,理由如下:
∵平行四边形ABCD,
∴AD∥BC,BO=DO,
∴∠FDO=∠EBO,∠DFO=∠BEO,
在△DFO和△BEO中
∵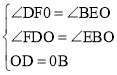 ,
,
∴△DFO≌△BEO(AAS),
∴OF=OE,
∴四边形BEDF是平行四边形,
∵AB=1,BC=![]() ,
,
∴在Rt△BAC中,由勾股定理得:AC=2,
∴AO=1=AB,
∴∠AOB=45°,
又∵∠AOF=45°,
∴∠BOF=90°,
∴BD⊥EF,
∴四边形BEDF是菱形,
即在旋转过程中,四边形BEDF能是菱形,此时AC绕点O顺时针旋转的度数是45°.



科目:初中数学 来源: 题型:
【题目】小刚根据以往的学习经验,想通过由“特殊到一般”的方法探究下面二次根式的运算规律.
以下是小刚的探究过程,请补充完整.
(1)具体运算,发现规律:
特例1:![]() ;特例2:
;特例2:![]() ;特例3:
;特例3:![]() ;
;
特例4:______(举一个符合上述运算特征的例子);
(2)观察、归纳,得出猜想:
如果![]() 为正整数,用含
为正整数,用含![]() 的式子表示这个运算规律:______;
的式子表示这个运算规律:______;
(3)请你证明猜想的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若1表示的点与﹣1表示的点重合,则﹣3表示的点与数 表示的点重合;
(2)若﹣1表示的点与3表示的点重合,回答以下问题:
①原点与数 表示的点重合;
②若数轴上A、B两点之间的距离为7,且A、B两点经折叠后重合,则A、B两点表示的数是
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
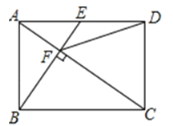
【题目】在矩形ABCD中,点E为AD的中点,连接BE、AC,AC⊥BE于点F,连接DF,对于结论①CF=2AF②△AEF∽△CAB③DF=DC④tan∠CAD=![]() 正确的有_______________.
正确的有_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约用水,某水厂规定:某单元居民如果一个月的用水量不超过![]() 吨,那么这个月该单元居民只交10元水费.如果超过
吨,那么这个月该单元居民只交10元水费.如果超过![]() 吨,则这个月除了仍要交10元水费外,超过那部分按每吨
吨,则这个月除了仍要交10元水费外,超过那部分按每吨![]() 元交费.
元交费.
(1)该单元居民8月份用水80吨,超过了“规定的![]() 吨”,则超过部分应交水费 (80-x)
吨”,则超过部分应交水费 (80-x)
元(用含x的式子表示).
(2)下表是该单元居民9月、10月的用水情况和交费情况:
月份 | 用水量(吨) | 交费总数(元) |
9月份 | 85 | 25 |
10月份 | 50 | 10 |
根据上表数据,求该x吨是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=x和![]() 的图象分别为直线l1、l2,过点A1(1,
的图象分别为直线l1、l2,过点A1(1,![]() )作x轴的垂线交l1于点A2,过点A2作y轴的垂线交l2于点A3,过点A3作x轴的垂线交l1于点A4,过点A4作y轴的垂线交l2于点A5,……依次进行下去,则点A2019的横坐标为( )
)作x轴的垂线交l1于点A2,过点A2作y轴的垂线交l2于点A3,过点A3作x轴的垂线交l1于点A4,过点A4作y轴的垂线交l2于点A5,……依次进行下去,则点A2019的横坐标为( )
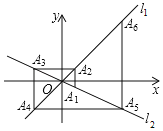
A.21008B.﹣21008C.﹣21009D.21006
查看答案和解析>>
科目:初中数学 来源: 题型:
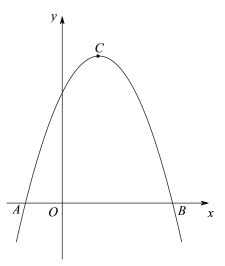
【题目】如图,在平面直角坐标系xOy中,二次函数![]() (a、b都是常数,且a<0)的图像与x轴交于点
(a、b都是常数,且a<0)的图像与x轴交于点![]() 、
、![]() ,顶点为点C.
,顶点为点C.
(1)求这个二次函数的解析式及点C的坐标;
(2)过点B的直线![]() 交抛物线的对称轴于点D,联结BC,求∠CBD的余切值;
交抛物线的对称轴于点D,联结BC,求∠CBD的余切值;
(3)点P为抛物线上一个动点,当∠PBA=∠CBD时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com