
 △ACD中,∠ACD=120°:
△ACD中,∠ACD=120°: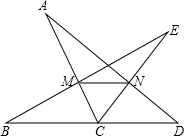 解:(1)所画图形如下所示:
解:(1)所画图形如下所示: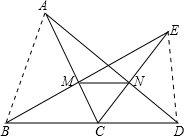
| NE |
| NC |
| ED |
| AC |
| EC |
| AB |
| ME |
| BM |


科目:初中数学 来源: 题型:
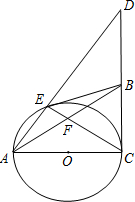 (2012•黄陂区模拟)如图,Rt△ACD中,∠ACD=90°.以AC边为直径作⊙O,交AD于E.过E作⊙O的切线EB,交CD于B.连接EC、AB,交于F点.
(2012•黄陂区模拟)如图,Rt△ACD中,∠ACD=90°.以AC边为直径作⊙O,交AD于E.过E作⊙O的切线EB,交CD于B.连接EC、AB,交于F点.| 1 |
| 2 |
| EF |
| FC |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 AB•CD,于是可将三角形面积公式变形,得S△ABC=______.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.
AB•CD,于是可将三角形面积公式变形,得S△ABC=______.①其文字语言表述为:三角形的面积等于两边及其夹角正弦积的一半.这就是我们将要在高中学习的正弦定理.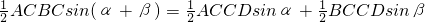 ,即
,即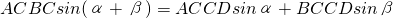 ②.
②.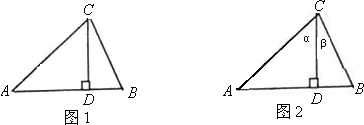
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
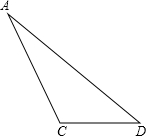 △ACD中,∠ACD=120°:
△ACD中,∠ACD=120°:查看答案和解析>>
科目:初中数学 来源:2009年江苏省连云港市中考数学原创试卷大赛(22)(解析版) 题型:解答题

 ,则AD=csinB
,则AD=csinB ,则AD=bsinC
,则AD=bsinC
 ,∠C=60°,求∠B的度数.
,∠C=60°,求∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com