
分析 分子、分母先进行因式分解化简,然后通分利用乘法公式化简.
解答 解:∵a>1
∴原式=$\frac{(\sqrt{a+1})^{2}+\sqrt{(a+1)(a-1)}}{(\sqrt{a+1})^{2}-\sqrt{(a+1)(a-1)}}$+$\frac{(\sqrt{a+1})^{2}-\sqrt{(a+1)(a-1)}}{(\sqrt{a+1})^{2}+\sqrt{(a+1)(a-1)}}$
=$\frac{\sqrt{a+1}+\sqrt{a-1}}{\sqrt{a+1}-\sqrt{a-1}}$+$\frac{\sqrt{a+1}-\sqrt{a-1}}{\sqrt{a+1}+\sqrt{a-1}}$
=$\frac{(\sqrt{a+1}+\sqrt{a-1})^{2}+(\sqrt{a+1}-\sqrt{a-1})^{2}}{(a+1)-(a-1)}$
=$\frac{4a}{2}$
=2a.
点评 本题考查二次根式的化简、乘法公式等知识,灵活运用公式化简是解题的关键.


科目:初中数学 来源: 题型:解答题
 已知如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
已知如图,直线MN交⊙O于A、B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 无数个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{ab}$ | D. | $\frac{1}{a-b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx过点A(4,0),正方形 OABC的边BC与抛物线的一个交点为D,点D的横坐标为3,点M在y轴负半轴上,直线l过点D、M两点且与抛物线的对称轴交于点H,tan∠OMD=$\frac{1}{3}$.
如图,抛物线y=ax2+bx过点A(4,0),正方形 OABC的边BC与抛物线的一个交点为D,点D的横坐标为3,点M在y轴负半轴上,直线l过点D、M两点且与抛物线的对称轴交于点H,tan∠OMD=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
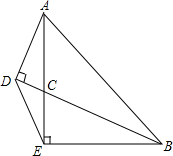 如图,△ABE中,∠AEB=90°,AE=BE,BC平分∠ABE交AE于C,AD⊥BC于D,连DE.
如图,△ABE中,∠AEB=90°,AE=BE,BC平分∠ABE交AE于C,AD⊥BC于D,连DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com