
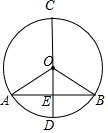
 如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为E,交⊙O于点C、D,
如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为E,交⊙O于点C、D,科目:初中数学 来源: 题型:选择题
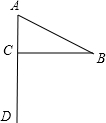 如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )
如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCA=90°.求解的直接依据是( )| A. | 三角形内角和定理 | B. | 三角形外角和定理 | ||
| C. | 多边形内角和公式 | D. | 多边形外角和公式 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )
如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
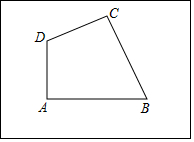 小亮家的房前有一块矩形的空地,空地上有四棵银杏树A、B、C,D,且∠A=∠C=90°,小亮想建一个圆形花坛,使四棵树都在花坛的边上.小亮请小明帮他设计方案:
小亮家的房前有一块矩形的空地,空地上有四棵银杏树A、B、C,D,且∠A=∠C=90°,小亮想建一个圆形花坛,使四棵树都在花坛的边上.小亮请小明帮他设计方案:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠A=∠B-∠C | B. | ∠A:∠B:∠C=1:3:4 | C. | $a:b:c=1:\sqrt{2}:3$ | D. | a2+c2=b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com