
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
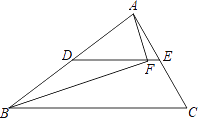
A.如图,DE为△ABC的中位线,点F为DE上一点,且∠AFB=90°,若AB=8,BC=10,则EF的长为________.
B.小智同学在距大雁塔塔底水平距离为138米处,看塔顶的仰角为24.8(不考虑身高因素),则大雁塔市约为________米.(结果精确到0.1米)
【答案】1 70.4
【解析】
A,首先根据三角形的中位线定理求得DE的长,然后利用直角三角形斜边上中线的性质可求得FD的长,则EF即可求得;
B、先作出图形,则AB=138米,∠A=24.8°,最后,在Rt△ABC中,利用三角函数的定义可求得BC的长.
A、∵DE为△ABC的中位线,
∴DE=![]() BC=
BC=![]() ×10=5,
×10=5,
∵∠AFB为直角,D是AB的中点,即FD是直角△ABF的中线,
∴FD=![]() AB=
AB=![]() ×8=4,
×8=4,
∴EF=DE﹣FD=5﹣4=1,
故答案是:1;
B、如图2,
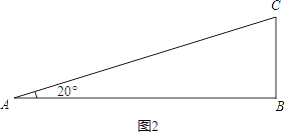
在Rt△ABC中,
AB=138米,∠BAC=24.8°,
∵![]() =tan24.8°,
=tan24.8°,
∴BC=ABtan24.8°≈138×0.51≈70.4(米).
故答案为:70.4.


科目:初中数学 来源: 题型:
【题目】已知:如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC与点D,AD的延长线交BC于点E,过D作⊙O的切线交BC于点F.下列结论:①CD2=CE·CB;②4EF 2=ED ·EA;③∠OCB=∠EAB;④![]() .其中正确的只有____________________.(填序号)
.其中正确的只有____________________.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AM是中线,D是AM所在直线上的一个动点(不与点A重合),DE∥AB交AC所在直线于点F,CE∥AM,连接BD,AE.

(1)如图1,当点D与点M重合时,观察发现:△ABM向右平移![]() BC到了△EDC的位置,此时四边形ABDE是平行四边形.请你给予验证;
BC到了△EDC的位置,此时四边形ABDE是平行四边形.请你给予验证;
(2)如图2,图3,图4,是当点D不与点M重合时的三种情况,你认为△ABM应该平移到什么位置?直接在图中画出来.此时四边形ABDE还是平行四边形吗?请你选择其中一种情况说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.
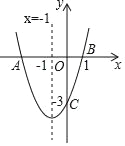
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小赵投资销售一种进价为每件20元的护眼台灯.销售过程中发现,当月内销售单价不变,则月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:![]() .
.
(1)设小赵每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?并求出最大利润.
(2)如果小赵想要每月获得的利润不低于2000元,那么如何制定销售单价才可以实现这一目标?
查看答案和解析>>
科目:初中数学 来源: 题型:
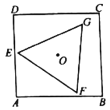
【题目】如图,正方形![]() 的边长为4,在这个正方形内作等边三角形
的边长为4,在这个正方形内作等边三角形![]() (三角形的顶点可以在正方形的边上),使它们的中心重合,则
(三角形的顶点可以在正方形的边上),使它们的中心重合,则![]() 的顶点到正方形
的顶点到正方形![]() 的顶点的最短距离是___________.
的顶点的最短距离是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 和
和![]() ,以下说法:
,以下说法:
①它们的图象都是开口向上;②它们的对称轴都是y轴,顶点坐标都是原点(0,0);③当x>0时,它们的函数y都是随x的增大而增大;④它们的开口的大小是一样的.
其中正确的说法有_______个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com