
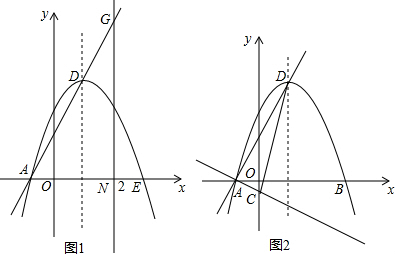
���� ��1����ȷ����������y��Ľ�������Ϊ��0��3����Ȼ�����ý���ʽ�������߽���ʽ���ٰѽ���ʽ��ɶ���ʽ���ɵõ�D�����ꣻ
��2����P��PH��AD�ڵ�H����ͼ1�����ô���ϵ�������ֱ��AD�Ľ���ʽΪy=2x+2����ȷ��G��2��6������P��2��t������PN=PH=|t|��GP=6-t���ù��ɶ��������AG=$\sqrt{5}$������֤��Rt��GPH��Rt��GAN���������Ʊȵõ�t�ķ��̣�6-t����3$\sqrt{5}$=|t|��3��Ȼ��ⷽ�����t���ɵõ�P�����ꣻ
��3����ȷ��ֱ��AC�Ľ���ʽΪy=-x-1������D��DE��AC����y���ڵ�E����ͼ2��������ֱ��ƽ����������ֱ��DE�Ľ���ʽΪy=-x+5����E��0��5�������ǿ�ȷ��EC���е�F������Ϊ��0��2�����ٹ���F��AC��ƽ���߽���������M����ͼ2������ƽ����֮��ľ�����жϵ�M��ֱ��AC�ľ�����ڵ�D��AC�ľ����һ�룬����S��CDA=2S��ACM������ȷ��ֱ��FM�Ľ���ʽΪy=-x+2��Ȼ��ⷽ����$\left\{\begin{array}{l}{y=-x+2}\\{y=-{x}^{2}+2x+3}\end{array}\right.$���ɵõ�����������M������꣮
��� �⣺��1����x=0ʱ��y=ax2+bx+3=3������������y��Ľ�������Ϊ��0��3����
�������߽���ʽΪy=a��x+1����x-3����
�ѣ�0��3�������a•1•��-3��=3�����a=-1��
���������߽���ʽΪy=-��x+1����x-3������y=-x2+2x+3��
y=-��x-1��2+4����D��1��4����
��2����P��PH��AD�ڵ�H����ͼ1��
��ֱ��AD�Ľ���ʽΪy=kx+p����A��-1��0����D��1��4�������$\left\{\begin{array}{l}{-k+b=0}\\{k+b=4}\end{array}\right.$�����$\left\{\begin{array}{l}{k=2}\\{b=2}\end{array}\right.$��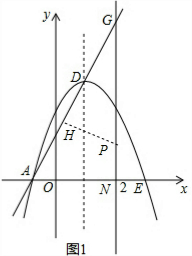
����ֱ��AD�Ľ���ʽΪy=2x+2��
��x=2ʱ��y=2x+2=6����G��2��6����
��P��2��t������PN=PH=|t|��GP=6-t��
��Rt��ANG��AN=3��GN=6��
��AG=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$��
�ߡ�PGH=��AGN��
��Rt��GPH��Rt��GAN��
��GP��AG=PH��AN������6-t����3$\sqrt{5}$=|t|��3��
���t1=$\frac{3\sqrt{5}-3}{2}$��t2=$\frac{-3\sqrt{5}-3}{2}$��
��P��������2��$\frac{3\sqrt{5}-3}{2}$����2��$\frac{-3\sqrt{5}-3}{2}$����
��3�����ڣ�
��A��-1��0������y=-x+m��1+m=0�����m=1��
��ֱ��AC�Ľ���ʽΪy=-x-1��
����D��DE��AC����y���ڵ�E����ͼ2��
��ֱ��DE�Ľ���ʽΪy=-x+n��
��D��1��4�������-1+n=4�����n=5��
��ֱ��DE�Ľ���ʽΪy=-x+5��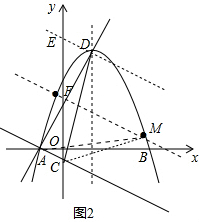
��x=0ʱ��y=-x+5=5����E��0��5����
��EC���е�F������Ϊ��0��2����
����F��AC��ƽ���߽���������M����ͼ2�����M��ֱ��AC�ľ�����ڵ�D��AC�ľ����һ�룬
��S��CDA=2S��ACM��
��ֱ��FM�Ľ���ʽΪy=-x+q��
��F��0��2�������q=2��
��ֱ��FM�Ľ���ʽΪy=-x+2��
�ⷽ����$\left\{\begin{array}{l}{y=-x+2}\\{y=-{x}^{2}+2x+3}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{3-\sqrt{13}}{2}}\\{y=\frac{1+\sqrt{13}}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{3+\sqrt{13}}{2}}\\{y=\frac{1-\sqrt{13}}{2}}\end{array}\right.$��
������������M���������$\frac{3-\sqrt{13}}{2}$��$\frac{1+\sqrt{13}}{2}$����
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ��������ʣ������ô���ϵ������������ʽ������һ�κ�������κ����Ľ������ꣻ����������ͼ�����ʣ������ù��ɶ��������Ʊȼ����߶εij���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
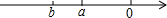 ����ʵ���������϶�Ӧ���λ����ͼ��ʾ����a��b�������������������=����
����ʵ���������϶�Ӧ���λ����ͼ��ʾ����a��b�������������������=�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����г���ţ�̵�������� | B�� | ����ȫ����Сѧ����������� | ||
| C�� | ����ijƷ�Ƶ��ݵ�ʹ������ | D�� | ���麽��ɻ��㲿���Ƿ�ϸ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 60�� | B�� | 90�� | C�� | 135�� | D�� | 180�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
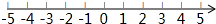
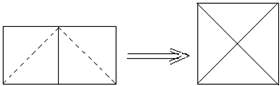
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com