
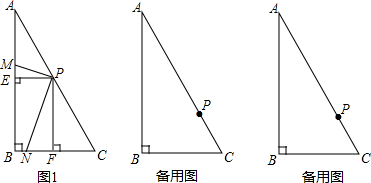
 如图,在梯形ABCD中,AD∥BC,∠B=45°,点E是AB的中点,DE=DC,∠EDC=90°,若AB=2,则AD的长是$\frac{\sqrt{2}}{2}$.
如图,在梯形ABCD中,AD∥BC,∠B=45°,点E是AB的中点,DE=DC,∠EDC=90°,若AB=2,则AD的长是$\frac{\sqrt{2}}{2}$. 分析 延长DE交CB的延长线于点F,将AD替换成BF,再由三角形相似,借助比的特性,即能得出结论.
解答 解:延长DE交CB的延长线于点F,如图,
∵AD∥BC,
∴∠ADE=∠F,
∵点E是AB的中点,
∴AE=BE=1,
在△ADE和△BFE中,$\left\{\begin{array}{l}{∠ADE=∠F}\\{∠AED=∠BEF(对顶角)}\\{AE=BE}\end{array}\right.$,
∴△ADE≌△BFE(AAS),
∴AD=BF,DE=EF,
∵∠B=∠F+∠BEF=45°,DE=DC,∠EDC=90°,
∴∠CED=∠F+∠ECF=45°,CE=$\sqrt{2}$DE,
∴∠BEF=∠ECF,
∵∠F=∠F,
∴△BEF∽△ECF,
∴$\frac{BF}{BE}$=$\frac{EF}{CE}$,即$\frac{BF}{EF}$=$\frac{BE}{CE}$,
∴$\frac{AD}{DE}$=$\frac{1}{\sqrt{2}DE}$,
∴AD=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查全等三角形的判定和性质以及相似三角形的判定和性质,解题的关键是巧妙的利用比的特性,化未知为已知,从而得出结论.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3m2n与3nm2 | B. | $-\frac{1}{4}{x^2}{y^{c+6}}$xy2与2x2+ay3x2y2 | ||
| C. | -5ab与-5×103ab | D. | 35与-12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{4}{2}$ | B. | $\sqrt{12}$ | C. | $\sqrt{0.2}$ | D. | $\sqrt{\frac{1}{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com