
分析 (1)认真观察题中所给的式子,得出其规律并根据规律写出第④个等式;
(2)根据规律写出含n的式子即可;
(3)结合二次根式的性质进行化简求解验证即可.
解答 解:(1)$\sqrt{4+\frac{1}{6}}$=5$\sqrt{\frac{1}{6}}$;
(2)$\sqrt{n+\frac{1}{n+2}}$=(n+1)$\sqrt{\frac{1}{n+2}}$;
(3)$\sqrt{n+\frac{1}{n+2}}$
=$\sqrt{\frac{{n}^{2}+2n}{n+2}+\frac{1}{n+2}}$
=$\sqrt{\frac{{n}^{2}+2n+1}{n+2}}$
=$\sqrt{\frac{(n+1)^{2}}{n+2}}$
=(n+1)$\sqrt{\frac{1}{n+2}}$.
故答案为:(1)$\sqrt{4+\frac{1}{6}}$=5$\sqrt{\frac{1}{6}}$;
(2))$\sqrt{n+\frac{1}{n+2}}$=(n+1)$\sqrt{\frac{1}{n+2}}$.
点评 本题考查了二次根式的性质与化简,解答本题的关键在于认真观察题中所给的式子,得出其规律并根据规律进行求解即可.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:解答题
 如图,抛物线y=a(x-1)2+k与x轴交于A、C两点,与y轴交于点B,点A、B的坐标分别为(-1,0)和(0,3).
如图,抛物线y=a(x-1)2+k与x轴交于A、C两点,与y轴交于点B,点A、B的坐标分别为(-1,0)和(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
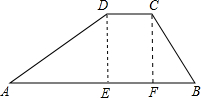 如图,水库大坝的横断面是梯形,坝顶宽是8m,坝高为30m.斜坡AD的坡度为i=$\sqrt{3}$:3,斜坡CB的坡度为i=2:3.求斜坡AD的坡角α,坝度宽AB和斜坡AD的长.
如图,水库大坝的横断面是梯形,坝顶宽是8m,坝高为30m.斜坡AD的坡度为i=$\sqrt{3}$:3,斜坡CB的坡度为i=2:3.求斜坡AD的坡角α,坝度宽AB和斜坡AD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
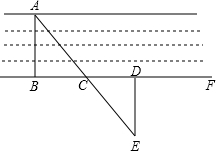 如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线,并在这条垂线上取一点E,使A、C、E在一条直线上(如图所示),测得ED的长就是A、B之间的距离,请你说明理由.
如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线,并在这条垂线上取一点E,使A、C、E在一条直线上(如图所示),测得ED的长就是A、B之间的距离,请你说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com