
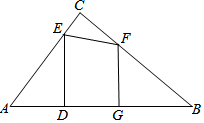
 如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.分析 (1)由△ADE∽△ACB,得$\frac{AD}{AC}$=$\frac{DE}{BC}$,由此即可解决问题.
(2)由△BGF∽△BCA,得$\frac{BG}{BC}$=$\frac{FG}{AC}$,由此即可解决问题.
(3)分两种情形①当∠A=∠CEF时,△ADE∽△ECF,$\frac{AD}{EC}$=$\frac{ED}{CF}$.②当∠A=∠CFE时,△ADE∽△FCE,$\frac{AD}{FC}$=$\frac{DE}{CE}$,分别列出方程即可解决问题.
解答 解:(1)∵∠ACB=90°,AB=10,AC=6
∴BC=8∵ED⊥AB,
∴∠ADE=∠ACB=90°
又∵∠A=∠A,
∴△ADE∽△ACB,
∴$\frac{AD}{AC}$=$\frac{DE}{BC}$,
∴$\frac{3}{6}$=$\frac{DE}{8}$,
∴DE=4.
(2)∵FG⊥AB,
∴∠BGF=∠BCA=90°,
又∵∠B=∠B,
∴△BGF∽△BCA,
∴$\frac{BG}{BC}$=$\frac{FG}{AC}$,
∴$\frac{8-x}{8}$=$\frac{y}{6}$,
∴y=-$\frac{3}{4}$x+6.
(3)由(1)(2)可得:AE=$\frac{5}{3}$x,BF=10-$\frac{5}{4}$x,
∴CE=6-$\frac{5}{3}$x,CF=$\frac{5}{4}$x-2,
当∠A=∠CEF时,△ADE∽△ECF,
∴$\frac{AD}{EC}$=$\frac{ED}{CF}$.
∴$\frac{x}{6-\frac{5}{3}x}$=$\frac{\frac{4}{3}x}{\frac{5}{4}x-2}$,
解得:x=$\frac{72}{25}$;
当∠A=∠CFE时,△ADE∽△FCE,
∴$\frac{AD}{FC}$=$\frac{DE}{CE}$,
∴$\frac{x}{\frac{5}{4}x-2}$=$\frac{\frac{4}{3}x}{6-\frac{5}{3}x}$,
解得:$\frac{13}{5}$,
∴当AD的长为$\frac{72}{25}$或$\frac{13}{5}$时△AED与△CEF相似.
点评 本题考查相似三角形综合题、解题的关键是记住相似三角形的判定方法,学会用方程的思想思考问题,学会分类讨论不能漏解,属于中考常考题型.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
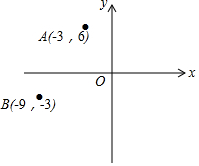 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为3:1,把△ABO放大,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为3:1,把△ABO放大,则点A的对应点A′的坐标是( )| A. | (-1,2) | B. | (-9,18) | C. | (-9,18)或(9,-18) | D. | (-1,2)或(1,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com