
分析 (1)设第一批玩具每套进价是x元,根据题意得出方程$\frac{2500}{x}$×1.5=$\frac{4500}{x+10}$,求出方程的解即可;
(2)第二批玩具每套售价是y元.,分别求出第一批购进玩具和第二批购进玩具,根据题意得出不等式,求出不等式的解集即可.
解答 解:(1)设第一批玩具每套进价是x元,根据题意得$\frac{2500}{x}$×1.5=$\frac{4500}{x+10}$,
解这个分试方程,得x=50,
经检验,x=50是原分式方程的解,且符合题意,
所以第一批玩具每套进价是50元;
(2)设第二批玩具每套售价是y元.第一批购进玩具$\frac{2500}{50}$=50(套),
第二批购进玩具50×1.5=75(套),
根据题意,得50(y-5)+75y-(2500+4500)≥(2500+4500)×25%,
解这个不等式,
得y≥72,
答:第二批玩具每套售价至少是72元.
点评 本题考查了分式方程的应用,解一元一次不等式等知识点,能根据题意列出方程或不等式是解此题的关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | -$\sqrt{13}$ | C. | $\frac{1}{\sqrt{13}}$ | D. | $\frac{1}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.
已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
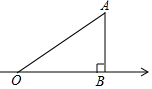 如图,在Rt△OAB中,∠ABO=90°,点O与原点重合,OB在数轴正半轴上,∠AOB=30°,AB=2,动点P从原点出发,在数轴正半轴上移动,当△OAP为等腰三角形时,P点表示的数是$\frac{4\sqrt{3}}{3}$或4或4$\sqrt{3}$.
如图,在Rt△OAB中,∠ABO=90°,点O与原点重合,OB在数轴正半轴上,∠AOB=30°,AB=2,动点P从原点出发,在数轴正半轴上移动,当△OAP为等腰三角形时,P点表示的数是$\frac{4\sqrt{3}}{3}$或4或4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD是∠BAC的平分线,且垂直于BC,垂足为D,点E在CA上,EG⊥BC,垂足为点G,交AB于点H.写出图中与∠CEG相等的所有角,并说明理由.
如图,AD是∠BAC的平分线,且垂直于BC,垂足为D,点E在CA上,EG⊥BC,垂足为点G,交AB于点H.写出图中与∠CEG相等的所有角,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成(4,3).
课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成(4,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com