
【题目】如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,ACB的顶点A在△ECD的斜边DE上 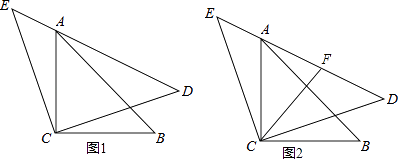
(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=2,AC=2 ![]() ,点F是AD的中点,直接写出CF的长是 .
,点F是AD的中点,直接写出CF的长是 .
【答案】
(1)证明:连结BD,如图所示:

∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,EC=DC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2.
∵∠ECD﹣ACD=∠ACB﹣∠ACD,
∴∠ACE=∠BCD.
在△AEC和△BDC中,  ,
,
∴△AEC≌△BDC(SAS).
∴AE=BD,∠E=∠BDC=45°,CE=CD,
∴∠BDA=∠BDC+∠ADC=90°,
在Rt△ADB中.∵AD2+BD2=AB2,
∴AD2+AE2=2AC2.
(2)2 ![]()
【解析】(2)解:由(1)得:CE=CD,AE2+AD2=2AC2; ∴∠E=∠CDA,22+AD2=2×(2 ![]() )2 ,
)2 ,
解得:AD=4,
∵点F是AD的中点,
∴AF=DF=2=AE,
∴EF=DA,
在△CEF和△CDA中,  ,
,
∴△CEF≌△CDA(SAS),
∴CF=CA=2 ![]() ;
;
所以答案是:2 ![]() .
.
【考点精析】通过灵活运用勾股定理的概念,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.


科目:初中数学 来源: 题型:
【题目】2015年我国大学生毕业人数将达到7 490 000人,这个数据用科学记数法表示为( )
A.7.49×107
B.7.49×106
C.74.9×105
D.0.749×107
查看答案和解析>>
科目:初中数学 来源: 题型:
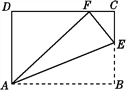
【题目】如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24 cm,△ECF的周长为8 cm,求四边形纸片ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
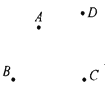
【题目】如图,豫东有四个村庄A、B、C、D.现在要建造一个水塔P.请回答水塔P应建在何位置,才能使它到4村的距离之和最小,说明最节约材料的办法和理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中( )
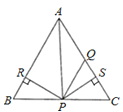
A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店有一种商品每件成本a元,原来成本增加22%定价售价,售出80件后,由于库存积压减价,按原来的85%出售,又增加120件.
(1)求该商品减价后的售价价格为多少元?
(2)售完200件这种商品是盈利还是亏损?若盈利共盈利了多少元?若亏损共亏损了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四舍五入法按要求对2.04607分别取近似值,其中错误的是( )
A.2(精确到个位)
B.2.05(精确到百分位)
C.2.1(精确到0.1)
D.2.0461(精确到0.0001)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.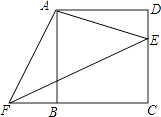
(1)求证:△ADE≌△ABF;
(2)若BC=12,DE=5,求△AEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com