
��ͼ1����֪������C����ԭ�㣬�Գ���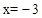 ���������ཻ�ڵ������ĵ�M����x���ཻ�ڵ�N����
���������ཻ�ڵ������ĵ�M����x���ཻ�ڵ�N����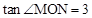 ��
��
��1����������C�Ľ���ʽ��
��2����������C��ԭ��O��ת1800�õ�������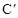 ��������
��������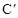 ��x�����һ����ΪA��BΪ������
��x�����һ����ΪA��BΪ������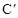 �Ϻ�����Ϊ2�ĵ㡣
�Ϻ�����Ϊ2�ĵ㡣
����PΪ�߶�AB��һ���㣬PD��y���ڵ�D�����APD��������ֵ��
�ڹ��߶�OA�ϵ�����E��F�ֱ���x��Ĵ��ߣ�������O��B��A��E1��F1���ٷֱ����߶�EE1��FF1Ϊ������ͼ2��ʾ�ĵȱߡ�AE1E2���ȱߡ�AF1F2����E��ÿ��1�����ȵ�λ���ٶȴӵ�O���A�˶�����F��ÿ��1�����ȵ�λ���ٶȴӵ�A���O�˶�������AE1E2��һ�����AF1F2��ijһ����ͬһֱ����ʱ����ʱ��t��ֵ��
�⣺��1���������ߵĶԳ���Ϊ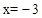 ����ON=3��
����ON=3��
��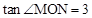 ����NM=9����M����3����9����
����NM=9����M����3����9����
����������C�Ľ���ʽΪ ��
��
��������C����ԭ�㣬�� ����
���� ��
��
��������C�Ľ���ʽΪ ����
���� ��
��
��2���١�������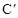 ��������C��ԭ��O��ת1800�õ���
��������C��ԭ��O��ת1800�õ���
��������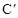 ��������C����ԭ��O�Գơ���������
��������C����ԭ��O�Գơ���������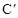 �Ķ�������Ϊ��3��9����
�Ķ�������Ϊ��3��9����
��������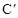 �Ľ���ʽΪ
�Ľ���ʽΪ ����
���� ��
��
����y=0����x=0��x=6����A��6��0����
�֡�BΪ������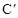 �Ϻ�����Ϊ2�ĵ㣬����x=2����y=8����B��2��8����
�Ϻ�����Ϊ2�ĵ㣬����x=2����y=8����B��2��8����
��ֱ��AB�Ľ���ʽΪy=kx+b��
�� ����ã�
����ã� ��
��
��ֱ��AB�Ľ���ʽΪ ��
��
��PΪ�߶�AB��һ���㣬����P ��
��
�� ��
��
APD��������ֵΪ9��
����ͼ���ֱ��E2��F2��x��Ĵ��ߣ�����ֱ�ΪG��H��
����ֱ��OB�� ���ɢ�ֱ��AB��
���ɢ�ֱ��AB�� ��
��
�� ʱ��E1��OB�ϣ�F1��AB�ϣ�
ʱ��E1��OB�ϣ�F1��AB�ϣ�
OE=t��EE1=4t��EG= ��OG=
��OG= ��GE2=2t��
��GE2=2t��
OF= ��FF1=2t��HF=
��FF1=2t��HF=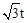 ��OH=
��OH= ��HF2= t��
��HF2= t��
��E��t��0����E1��t��4t����E2�� ��2t����F��6��t��0����F1��
��2t����F��6��t��0����F1�� ��2t����F2��
��2t����F2�� ��t����
��t����
i����EE1��FF1��ͬһֱ���ϣ���t=6��t��t=3�������� ��
��
ii����EE2��F1F2��ͬһֱ���ϣ������EE2�� ����F1��
����F1�� ��2t�����룬��
��2t�����룬�� �����
����� ��
��
iii����E1E2��FF2��ͬһֱ���ϣ������E1E2�� ����F��
����F�� ��0�����룬��
��0�����룬�� ��
��
�� ʱ��E1��F1����AB�ϣ�
ʱ��E1��F1����AB�ϣ�
OE=t��EE1= ��EG=
��EG= ��OG=
��OG= ��GE2=
��GE2= ��
��
OF= ��FF1=2t��HF=
��FF1=2t��HF=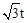 ��OH=
��OH= ��HF2= t��
��HF2= t��
��E��t��0����E1��t�� ����E2��
����E2�� ��
�� ����F��
����F�� ��0����F1��
��0����F1�� ��2t����F2��
��2t����F2�� ��t����
��t����
i����EE1��FF1��ͬһֱ���ϣ���t=6��t��t=3��
ii����EE2��F1F2��ͬһֱ���ϣ������EE2�� ����F1��
����F1�� ��2t�����룬��
��2t�����룬�� �����
����� ��������
�������� ��
��
iii��E1E2��FF2���� ʱ��ͬһֱ���ϣ��ʵ�
ʱ��ͬһֱ���ϣ��ʵ� ʱE1E2��FF2��������ͬһֱ���ϡ�
ʱE1E2��FF2��������ͬһֱ���ϡ�
�� ʱ�����������۵Ľ������AE1E2��һ�����AF1F2��ijһ�߲�������ͬһֱ���ϡ�
ʱ�����������۵Ľ������AE1E2��һ�����AF1F2��ijһ�߲�������ͬһֱ���ϡ�
��������������AE1E2��һ�����AF1F2��ijһ����ͬһֱ����ʱ�� ��
������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���κ���ͼ��Ķ����ǣ�-1��2�����ҹ��㣨0�� ����
����
��1������κ����ı���ʽ������ͼ�л�������ͼ��
��2���жϵ㣨2�� ���Ƿ��ڸö��κ���ͼ���ϣ���ָ����
���Ƿ��ڸö��κ���ͼ���ϣ���ָ���� ȡ��ֵʱ��
ȡ��ֵʱ��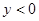 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�������� ��ֱ��
��ֱ�� ���ڵ�A ��B����y�ύ�ڵ�C��
���ڵ�A ��B����y�ύ�ڵ�C��
��1�����A��B�����ꣻ
��2������P��ֱ��x=1��һ�㣬�Ƿ���ڡ�PAB�ǵ��������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��Ҫ���һ�����εĻ�̳����̳��60 m����40 m����������������һ������������������������������Բ����������Բ���������ڰ�Բ�İ뾶Ϊ10 m���������Ŀ����������������ȵ�2������������Ŀ�Ϊ2x m�����е�ֵȡ3��
��1���ú�x��ʽ�ӱ�ʾ������Բ�����������֮�ͣ�
��2���������������֮�ͱȾ�������� ��36 m2ʱ����x��ֵ��
��36 m2ʱ����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ʡij��һ���������ι��ţ��Ź�����ֱƽ���ڣ���ˮƽ�����ཻ��A��B���㣬�Ź���ߵ�C��AB�ľ���Ϊ9m��AB=36m��D��EΪ�Ź��ײ������㣬��DE��AB����E��ֱ��AB�ľ���Ϊ7m����DE�ij�Ϊ�� ��m. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵxOy�У������� �Ķ���ΪA����y��Ľ���ΪB������AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹAD=AC������BD����AE��x�ᣬDE��y�ᣮ
�Ķ���ΪA����y��Ľ���ΪB������AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹAD=AC������BD����AE��x�ᣬDE��y�ᣮ
��1����m=2ʱ�����B�����ꣻ
��2����DE�ij���
��3�������D������Ϊ��x��y������y����x�ĺ�����ϵʽ���ڹ���D��AB��ƽ���ߣ���ڣ�3������ȷ���ĺ���ͼ�����һ������ΪP����mΪ��ֵʱ���ԣ�A��B��D��PΪ������ı�����ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�������� ��y�ύ�ڵ�C��0����4������x�ύ�ڵ�A��B����B�������Ϊ��2��0��
��y�ύ�ڵ�C��0����4������x�ύ�ڵ�A��B����B�������Ϊ��2��0��
��1����������ߵĽ���ʽ��
��2������P��AB�ϵ�һ���㣬����P��PE��AC����BC��E������CP�����PCE��������ֵ��
��3������DΪOA���е㣬��M���߶�AC��һ�㣬�ҡ�OMDΪ���������Σ���M������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪������ ��ͼ����x���һ������ΪB��5��0������һ������ΪA������y�ύ�ڵ�C��0��5����
��ͼ����x���һ������ΪB��5��0������һ������ΪA������y�ύ�ڵ�C��0��5����
��1����ֱ��BC�������ߵĽ���ʽ��
��2������M����������x���·�ͼ���ϵĶ��㣬����M��MN��y�ύֱ��BC�ڵ�N����MN�����ֵ��
��3���ڣ�2���������£�MNȡ�����ֵʱ������P����������x���·�ͼ��������һ�㣬��BCΪ����ƽ���ı���CBPQ����ƽ���ı���CBPQ�����ΪS1����ABN�����ΪS2����S1=6S2�����P�����ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪�����߾���A����2��0����B����3��3����ԭ��O������ΪC
��1���������ߵĺ�������ʽ��
��2�����D���������ϣ���E�������ߵĶԳ����ϣ�����AOΪ�ߵ��ı���AODE��ƽ���ı��Σ����D�����꣮
��3��P���������ϵ�һ�����ڵĶ��㣬����P��PM��x�ᣬ����ΪM���Ƿ���ڵ�P��ʹ����P��M��AΪ��������������BOC���ƣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com