
【题目】如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE,AB=CD=6,AD=BC=10,试求EC的长度. 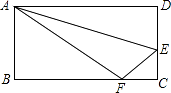
【答案】解:∵△AFE是由△ADE折叠得到, ∴AF=AD=10cm,FE=DE,
在Rt△ABF中,BF= ![]() =
= ![]() =8cm,
=8cm,
∴CF=2cm,
设CE=xcm,则FE=DE=(6﹣x)cm,
在Rt△FCE中,FE2=EC2+FC2 , 即(6﹣x)2=22+x2 ,
解得x= ![]() ,
,
即CE= ![]() cm
cm
【解析】由四边形ABCD为矩形,AB=6cm,BC=10cm,又由折叠的性质,即可得AF=AD,然后在Rt△ABF中,利用勾股定理求得BF的长,即可得CF的长,然后设CE=xcm,在Rt△FCE中,由勾股定理即可得方程:(6﹣x)2=22+x2 , 解此方程即可求得CE的长
【考点精析】本题主要考查了勾股定理的概念和翻折变换(折叠问题)的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】计算
(1)27﹣19+(﹣7)﹣32;
(2)(﹣7)÷(﹣ ![]() )×(﹣
)×(﹣ ![]() );
);
(3)( ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣36)
)×(﹣36)
(4)﹣14﹣ ![]() ×[2﹣(﹣3)2].
×[2﹣(﹣3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年1月1日零点,北京、上海、重庆、宁夏的气温分别是﹣4℃、5℃、6℃、﹣8℃,当时这四个城市中,气温最低的是( )
A.北京
B.上海
C.重庆
D.宁夏
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与x轴、y轴分别交于点A、B,与一次函数y2=x的图象交于点M,点A的坐标为(6,0),点M的横坐标为2,过点P(a,0),作x轴的垂线,分别交函数y=kx+b和y=x的图象于点C、D. 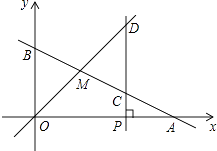
(1)求一次函数y1=kx+b的表达式;
(2)若点M是线段OD的中点,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
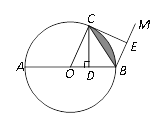
【题目】如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D, 过点B作BM∥OC,在射线BM上取点E, 使BE=BD,连接CE.
(1) 当∠COB=60° 时,直接写出阴影部分的面积;
(2) 求证:CE是 ⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com