
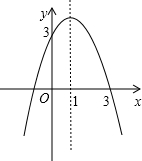
 已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题:
已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题:


科目:初中数学 来源: 题型:
 如图,给出下列条件:①∠3=∠4;②∠1=∠2;③EF∥CD,且∠D=∠4;④∠3+∠5=180°.其中,能推出AD∥BC的条件为( )
如图,给出下列条件:①∠3=∠4;②∠1=∠2;③EF∥CD,且∠D=∠4;④∠3+∠5=180°.其中,能推出AD∥BC的条件为( )| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则sin∠B′的值为( )
如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则sin∠B′的值为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 某中学举行的科普知识竞赛中,将初三四个班级的参赛学生的成绩(得分均为正整数)进行整理后分成五组,绘制出图如下.从左到右的第二小组的频率是0.4.
某中学举行的科普知识竞赛中,将初三四个班级的参赛学生的成绩(得分均为正整数)进行整理后分成五组,绘制出图如下.从左到右的第二小组的频率是0.4.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC中,AB=AC,∠BAC=70°,P为BC上一点,将△ABP绕点A按逆时针方向旋转到△ACP′位置,则∠AP′P的度数为( )
如图,△ABC中,AB=AC,∠BAC=70°,P为BC上一点,将△ABP绕点A按逆时针方向旋转到△ACP′位置,则∠AP′P的度数为( )| A、30° | B、60° |
| C、45° | D、55° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com