
| BE |
| CD |
| CB |
| CH |
| EA |
| AD |
| BC |
| CF |
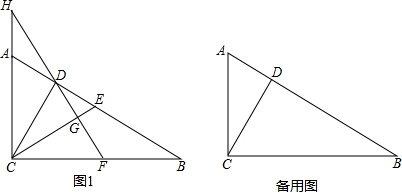
 解:(1)如图1,
解:(1)如图1,| BE |
| CD |
| CB |
| CH |
| EA |
| DC |
| AC |
| CF |
| BC |
| AC |
| CD |
| AD |
| EA |
| AD |
| BC |
| CF |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 某公司举办汇演,安排了一个“抽奖“环节;在一个不透明的盒子里,放入4个除颜色外均相等的彩球,其中红球2个,黄球1个,篮球1个,每人一次从盒子中任意摸出两个球.
某公司举办汇演,安排了一个“抽奖“环节;在一个不透明的盒子里,放入4个除颜色外均相等的彩球,其中红球2个,黄球1个,篮球1个,每人一次从盒子中任意摸出两个球.| 类型 | 两红 | 一红一黄 | 一红一蓝 | 一黄一蓝 |
| 价值 | 200元 | 150元 | 100元 | 50元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
A、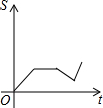 |
B、 |
C、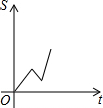 |
D、 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com