
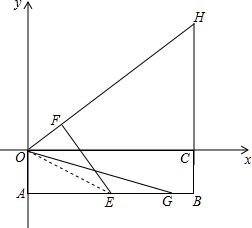
 如图,矩形OABC中,OA在y轴的负半轴上,OC在x轴的正半轴上,OA=1,OC=4,E是AB的中点,将矩形沿OE折叠,点A与点F重合,延长OF、BC交于点H,G是射线AB上一点,将△OAG绕点O旋转,使得点A落在OE上,记旋转后的三角形为△OA′G′,A′G′与OH交于点M,若∠MHG′=∠MHB,则AG的长为$\frac{2+20\sqrt{5}}{11}$.
如图,矩形OABC中,OA在y轴的负半轴上,OC在x轴的正半轴上,OA=1,OC=4,E是AB的中点,将矩形沿OE折叠,点A与点F重合,延长OF、BC交于点H,G是射线AB上一点,将△OAG绕点O旋转,使得点A落在OE上,记旋转后的三角形为△OA′G′,A′G′与OH交于点M,若∠MHG′=∠MHB,则AG的长为$\frac{2+20\sqrt{5}}{11}$. 分析 先求出DF,再由△DOE∽△HOC,求出CH,OH,然后用△COH∽△NG′H,求出MN,G′M,最后AG=A′M+G′M即可.
解答 解:如图,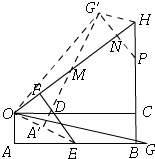
连接G′H,作G′P⊥OH,
根据折叠的性质得,△OAE≌△OFE,
∴OP=OA=1,EF=AE=2,∠AEO=∠FEO,
∵OC∥AB,
∴∠DOE=∠AEO=∠FEO,
∴OD=OE,
设OD=OE=x,
∴DF=2-x,
根据勾股定理得,OD2=OF2+DF2,
∴x2=1+(2-x)2,
∴x=$\frac{5}{4}$,
∴DF=2-x=$\frac{3}{4}$,
∵△DOE∽△HOC,
∴$\frac{CH}{DF}=\frac{OC}{OF}$,
∴$\frac{CH}{\frac{3}{4}}=4$,
∴CH=3,
∴OH=5,
根据旋转得,OA′=OA=OF=1,
∴△EOF≌△MOA′,
∴OM=OE=$\sqrt{5}$,A′M=EF=2,
∵∠MH′=∠MHB,G′P⊥OH,
∴△PHG′是等腰三角形,
∴NG′=PN,
设MN=x,
∴NH=5-$\sqrt{5}$-x,
∵△COH∽△NG′H,
∴$\frac{NH}{CH}=\frac{NG′}{OC}$,
∴$\frac{5-\sqrt{5}-x}{3}=\frac{NG′}{4}$,
∴NG′=$\frac{4(5-\sqrt{5}-x)}{3}$,
∵△A′OM∽△NG′M,
∴$\frac{NG′}{OA′}=\frac{MN}{A′M′}$,
∴$\frac{\frac{4(5-\sqrt{5}-x)}{3}}{1}=\frac{x}{2}$,
∴x=$\frac{40-8\sqrt{5}}{11}$,
∴MN=$\frac{40-8\sqrt{5}}{11}$,
∴$\frac{G′M}{OM}=\frac{MN}{A′M}$,
∴$\frac{G′M}{\sqrt{5}}=\frac{40-8\sqrt{5}}{22}$,
∴G′M=$\frac{20\sqrt{5}-20}{11}$,
∴AG=A′G′=A′M+G′M=2+$\frac{20\sqrt{5}-20}{11}$=$\frac{2+20\sqrt{5}}{11}$,
故答案为$\frac{2+20\sqrt{5}}{11}$.
点评 此题是折叠问题,主要考查了折叠,旋转的性质,相似三角形的性质和判定,解本题的关键是利用相似求出OD,DF.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{a-b}$ | B. | $\frac{1}{b-a}$ | C. | a-b | D. | b-a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
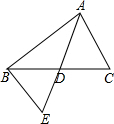 如图,△ABC中,AD是中线,将△ACD旋转后能与△EBD重合.
如图,△ABC中,AD是中线,将△ACD旋转后能与△EBD重合.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
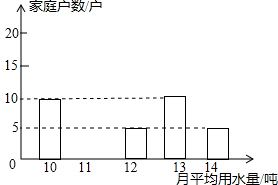 为了倡导“节约用水,从我做起”,南沙区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中50户家庭一年的月平均用水量(单位:吨),调查中发现每户用水量均在10-14吨/月范围,并将调查结果制成了如图所示的条形统计图.
为了倡导“节约用水,从我做起”,南沙区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中50户家庭一年的月平均用水量(单位:吨),调查中发现每户用水量均在10-14吨/月范围,并将调查结果制成了如图所示的条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com