
【题目】把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( )

A. 6→3 B. 7→16 C. 7→8 D. 6→15
【答案】D
【解析】
根据轴对称图形和中心对称图形的定义逐项识别即可,在平面内,一个图形经过中心对称能与原来的图形重合,这个图形叫做叫做中心对称图形。一个图形的一部分,以某条直线为对称轴,经过轴对称能与图形的另一部分重合,这样的图形叫做轴对称图形.
6→3 ,能使它与其余四个阴影部分的正方形组成一个轴对称图形,但不是中心对称图形 ,故不符合题意;
B. 7→16,能使它与其余四个阴影部分的正方形组成一个中心对称图形,但不是轴对称图形,故不符合题意;
C. 7→8 ,能使它与其余四个阴影部分的正方形组成一个轴对称图形,但不是中心对称图形,故不符合题意;
D. 6→15,能使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,故符合题意;
故选:D.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】我们用f(x)表示不大于x的最大整数,例如:f(2.3)=2,f(4)=4,f(﹣1.5)=﹣2;用g(y)表示不小于y的最小整数.例如:g(2.5)=3,g(5)=5,g(﹣3.5)=﹣3.解决下列问题:
(1)根据以上运算规律:f(﹣5.4)=______,g(4.5)=______.
(2)若f(x)=3,则x的取值范围是_______;若g(y)=﹣2,则y的取值范围是______.
(3)已知x,y满足![]() ,求x,y的取值范围.
,求x,y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长是4,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:
 =
= =
=![]() =
=![]() -2;
-2;
 =
= =
=![]() .
.
请回答下列问题:
(1)观察上面的解题过程,请直接写出式子![]() = ;
= ;
(2)观察上面的解题过程,请直接写出式子![]() = ;
= ;
(3)利用上面所提供的解法,请求![]() +···+
+···+![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.

(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是______数(填“无理”或“有理”),这个数是______;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是______;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,-1,-5,+4,+3,-2当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
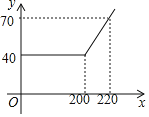
【题目】某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200小时”,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.
(1)当x≥200时,求y与x之间的函数关系式
(2)若小刚家10月份上网180小时,则他家应付多少元上网费?
(3)若小明家10月份上网费用为52元,则他家该月的上网时间是多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商城销售A,B两种自行车.A型自行车售价为2 100元/辆,B型自行车售价为1 750元/辆,每辆A型自行车的进价比每辆B型自行车的进价多400元,商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等.
(1)求每辆A,B两种自行车的进价分别是多少?
(2)现在商城准备一次购进这两种自行车共100辆,设购进A型自行车m辆,这100辆自行车的销售总利润为y元,要求购进B型自行车数量不超过A型自行车数量的2倍,总利润不低于13 000元,求获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y1=ax2﹣![]() x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,
x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,![]() ),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.

(1)求抛物线y2的解析式;
(2)如图2,在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出所有点T的坐标;若不存在,请说明理由;
(3)点P为抛物线y1上一动点,过点P作y轴的平行线交抛物线y2于点Q,点Q关于直线l的对称点为R,若以P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )

A. ![]() B. 4 C.
B. 4 C. ![]() D. 5
D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com