
【题目】等边△ABC中,点H在边BC上,点K在边AC上,且满足AK=HC,连接AH、BK交于点F,

(1)如图1,求∠AFB的度数;
(2)如图2,连接FC,若∠BFC=90°,点G为边 AC上一点,且满足∠GFC=30°,求证:AG⊥BG;
【答案】(1) ![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)易得:![]() ≌
≌ ![]()
![]() 即可求出
即可求出![]() 的度数.
的度数.
(2))在BF上取M使AF=FM,连MC延长FG交MC于N,可得△AFM是等边三角形,可证△AFB≌△AMC,再证△AGF≌△CGN,可得![]() 是
是![]() 的中点,可以根据等腰三角形三线合一的性质解答即可.
的中点,可以根据等腰三角形三线合一的性质解答即可.
解:(1)在等边△ABC中:AB=AC,∠BAK=∠C=60°
在△ABK和△CAH中,
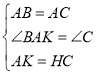
∴![]() ≌
≌ ![]()
![]()
![]()
(2)在BF上取M使AF=FM,连MC延长FG交MC于N,
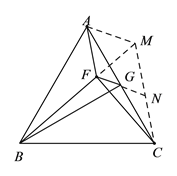
∵![]()
∴![]()
∴△AFM是等边三角形
∴AF=AM, ∠FAM=60°
又∵∠BAC=60°
∴∠BAF=∠CAM
又∵AB=AC
∴△AFB≌△AMC,
∴∠AMC=∠AFC= 120°,
又△AFM为等边三角形,
∴∠AMB=∠BMC=60°,
∵∠BFC=90°,
∴∠MFC=90°,∠NFC=30°,
∴△FMN为等边三角形,且FN=NC,
∴NC=FN=FM=AF,
∴△AGF≌△CGN,
∴AG=GC,
又∵AB=BC
∴BG⊥AC,


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,对称轴是直线x=-![]() ,有下列结论:(1)ab>0;(2)a+b+c<0;(3)b+2c<0;(4)a-2b+4c>0.其中正确结论的个数是( )
,有下列结论:(1)ab>0;(2)a+b+c<0;(3)b+2c<0;(4)a-2b+4c>0.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BF是AC边上中线,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,∠CFE的大小是( )

A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.

(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市从 2018 年 1 月 1 日开始,禁止燃油助力车上路,于是电动自 行车的市场需求量日渐增多.某商店计划最多投入 8 万元购进 A、B 两种型号的 电动自行车共 30 辆,其中每辆 B 型电动自行车比每辆 A 型电动自行车多 500 元.用 5 万元购进的 A 型电动自行车与用 6 万元购进的 B 型电动自行车数量一 样.
(1)求 A、B 两种型号电动自行车的进货单价;
(2)若 A 型电动自行车每辆售价为 2800 元,B 型电动自行车每辆售价为 3500 元,设该商店计划购进 A 型电动自行车 m 辆,两种型号的电动自行车全部销售 后可获利润 y 元.写出 y 与 m 之间的函数关系式;
(3)该商店如何进货才能获得最大利润?此时最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现场学习题:
问题背景:
在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.
,求这个三角形的面积.
小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.

(1)请你将△ABC的面积直接填写在横线上. .
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法,若△ABC三边的长分别为![]() a,2
a,2![]() a、
a、![]() a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .
a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .
探索创新:
(3)若△ABC三边的长分别为![]() 、
、![]() 、
、![]() (m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: .
(m>0,n>0,m≠n),请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点A,经过点A的抛物线y=ax2﹣3x+c的对称轴是x=
与x轴交于点A,经过点A的抛物线y=ax2﹣3x+c的对称轴是x=![]() .
.
(1)求抛物线的解析式;
(2)平移直线l经过原点O,得到直线m,点P是直线m上任意一点,PB⊥x轴于点B,PC⊥y轴于点C,若点E在线段OB上,点F在线段OC的延长线上,连接PE,PF,且PE=3PF.求证:PE⊥PF;
(3)若(2)中的点P坐标为(6,2),点E是x轴上的点,点F是y轴上的点,当PE⊥PF时,抛物线上是否存在点Q,使四边形PEQF是矩形?如果存在,请求出点Q的坐标,如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com