
 某学校矩形数学家“摇篮杯”会徽设计大赛,小明设计的会徽如图所示.正△DEF和正△GMN均由正△ABC平移得到,点A,B,M,N,F,D在正△RST边上,EC=2BE.若阴影部分的面积为$\frac{5\sqrt{3}}{32}$,则正△RST的边长是$\frac{5}{4}$.
某学校矩形数学家“摇篮杯”会徽设计大赛,小明设计的会徽如图所示.正△DEF和正△GMN均由正△ABC平移得到,点A,B,M,N,F,D在正△RST边上,EC=2BE.若阴影部分的面积为$\frac{5\sqrt{3}}{32}$,则正△RST的边长是$\frac{5}{4}$. 分析 过点G作GH⊥CE于点H,连接AD,过点R作RK⊥AD于点K,设正△GMN的边长为2x,则BE=x,RS=5x,再由阴影部分的面积求出x的值,进而可得出结论.
解答  解:过点G作GH⊥CE于点H,连接AD,过点R作RK⊥AD于点K,设正△GMN的边长为2x,则BE=x,RS=5x,
解:过点G作GH⊥CE于点H,连接AD,过点R作RK⊥AD于点K,设正△GMN的边长为2x,则BE=x,RS=5x,
∵GH⊥CE,RK⊥AD,
∴GH=EG•sin60°=2x•$\frac{\sqrt{3}}{2}$=$\sqrt{3}$x,RK=$\frac{\sqrt{3}}{2}$x,
∵阴影部分的面积为$\frac{5\sqrt{3}}{32}$,
∴S△EGC+3S菱形AGDR=$\frac{1}{2}$•2x•$\sqrt{3}$x+3x•$\frac{\sqrt{3}}{2}$x=$\frac{5\sqrt{3}}{32}$,
解得x=$\frac{1}{4}$,
∴正△RST的边长=5x=$\frac{5}{4}$.
故答案为:$\frac{5}{4}$.
点评 本题考查的是利用平移设计图案,熟知图形平移不变性的性质是解答此题的关键.


科目:初中数学 来源: 题型:填空题
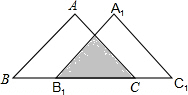 如图,将等腰直角△ABC沿BC方向平移得到△A1B1C1.若B1C=3$\sqrt{2}$.△ABC与△A1B1C1重叠部分面积为$\frac{9}{2}$.
如图,将等腰直角△ABC沿BC方向平移得到△A1B1C1.若B1C=3$\sqrt{2}$.△ABC与△A1B1C1重叠部分面积为$\frac{9}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,放入六个形状,大小相同的长方形(即空白的长方形),AD=16cm,FG=4cm,则图中阴影部分的总面积是82 cm2.
如图,在矩形ABCD中,放入六个形状,大小相同的长方形(即空白的长方形),AD=16cm,FG=4cm,则图中阴影部分的总面积是82 cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
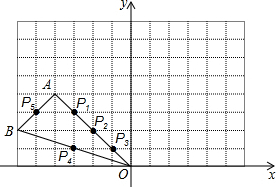 如图,在边长为1的小正方形组成的网格中,△AOB的顶点都在格点上,点A、B的坐标分别为(-4,4)、(-6,2).请按要求完成下列各题:
如图,在边长为1的小正方形组成的网格中,△AOB的顶点都在格点上,点A、B的坐标分别为(-4,4)、(-6,2).请按要求完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com