
分析 (1)原式根据阅读材料中的方法化简即可;
(2)原式根据阅读材料中的方法化简即可;
(3)原式各项根据阅读材料中的方法化简即可.
解答 解:(1)原式=$\frac{\sqrt{5}}{\sqrt{5}×\sqrt{5}}$=$\frac{\sqrt{5}}{5}$;
(2)原式=$\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}$=$\sqrt{5}$-$\sqrt{3}$;
(3)原式=$\frac{1}{2}$($\sqrt{3}$-1+$\sqrt{5}$-$\sqrt{3}$+$\sqrt{7}$-$\sqrt{5}$+…+$\sqrt{2n+1}$-$\sqrt{2n-1}$)=$\frac{\sqrt{2n+1}-1}{2}$.
故答案为:(1)$\frac{\sqrt{5}}{5}$;(2)$\sqrt{5}$-$\sqrt{3}$
点评 此题考查了分母有理化,弄清材料中的分母有理化方法是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC=7,BC=5,AF⊥BC于F,BE⊥AC于E,D是AB的中点,则△DEF的周长是$\frac{19}{2}$.
如图,在△ABC中,AB=AC=7,BC=5,AF⊥BC于F,BE⊥AC于E,D是AB的中点,则△DEF的周长是$\frac{19}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
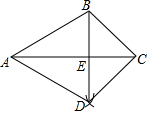 如图,已知△ABC,按如下步骤作图:
如图,已知△ABC,按如下步骤作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
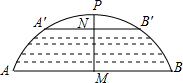 如图所示,有一座拱桥圆弧形,它的跨度AB为60米,拱高PM为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施,若拱顶离水面只有4米,即PN=4米时,是否采取紧急措施?($\sqrt{2}$=1.414)
如图所示,有一座拱桥圆弧形,它的跨度AB为60米,拱高PM为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施,若拱顶离水面只有4米,即PN=4米时,是否采取紧急措施?($\sqrt{2}$=1.414)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
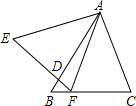 如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E.AB交EF于D.给出下列结论:
如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E.AB交EF于D.给出下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
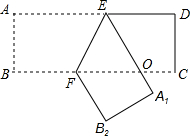 如图,把一张长方形纸片ABCD沿EF折叠后,点A、B分别落在A1、B2的位置上,A1E与BC交于点O,若∠EFO=60°,则∠AEA1=120°.
如图,把一张长方形纸片ABCD沿EF折叠后,点A、B分别落在A1、B2的位置上,A1E与BC交于点O,若∠EFO=60°,则∠AEA1=120°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com