练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（1，0）和B，与y轴的正半轴交于点C，下列结论：①abc＞0；②4a﹣2b+c＞0；③2a﹣b＞0，其中正确的个数为（　　）

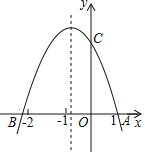
    A.0个B.1个C.2个D.3个

    【答案】C

    【解析】

    由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，进而判断①；根据x=﹣2时，y＞0可判断②；根据对称轴x=﹣1求出2a与b的关系，进而判断③．

    ①由抛物线开口向下知a＜0，

    ∵对称轴位于y轴的左侧，

    ∴a、b同号，即ab＞0．

    ∵抛物线与y轴交于正半轴，

    ∴c＞0，

    ∴abc＞0；

    故①正确；

    ②如图，当x=﹣2时，y＞0，则4a﹣2b+c＞0，

    故②正确；

    ③∵对称轴为x=﹣＞﹣1，

    ∴2a＜b，即2a﹣b＜0，

    故③错误；

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

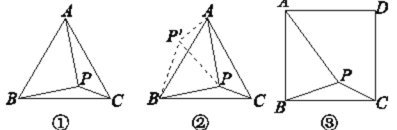
    【题目】问题：如图①，在等边三角形ABC内有一点P，且PA＝2，PB=，PC＝1，求∠BPC的度数和等边三角形ABC的边长．

    李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形(如图②)，连接PP′，可得△P′PB是等边三角形，而△PP′A又是直角三角形(由勾股定理的逆定理可证)，可得∠AP′B＝ °，所以∠BPC＝∠AP′B＝ °，还可证得△ABP是直角三角形，进而求出等边三角形ABC的边长为 ，问题得到解决．

    （1）根据李明同学的思路填空：∠AP′B＝ °，∠BPC＝∠AP′B＝ °，等边三角形ABC的边长为 ．

    （2）探究并解决下列问题：如图③，在正方形ABCD内有一点P，且PA＝，PB＝，PC＝1.求∠BPC的度数和正方形ABCD的边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

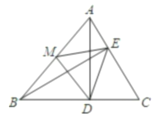
    【题目】如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，M为AB边的中点，连结ME、MD、ED，设AB=10，∠DBE=30°，则△EDM的面积为____________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0）、B两点，与y轴交于点C （0，3），点P在该抛物线的对称轴上，且纵坐标为2．

    （1）求抛物线的表达式以及点P的坐标；

    （2）当三角形中一个内角α是另一个内角β的两倍时，我们称α为此三角形的“特征角”．

    ①当D在射线AP上，如果∠DAB为△ABD的特征角，求点D的坐标；

    ②点E为第一象限内抛物线上一点，点F在x轴上，CE⊥EF，如果∠CEF为△ECF的特征角，求点E的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

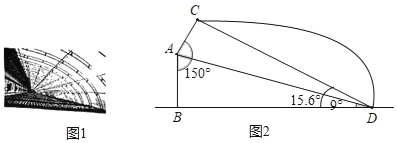
    【题目】河南省政府为促进农业发展，加快农村建设，计划扶持兴建一批新型钢管装配式大棚，如图1所示线段AB、BD分别为大棚的墙高和跨度，AC表示保温板的长，已知墙高AB为3米，墙面与保温板所成的角∠BAC＝150°，在点D处测得A点、C点的仰角分别为9°，15．6°，如图2所示求保温板AC的长是多少米？（精确到0.1米）（参考数据：sin9°≈0.16，cos9°≈0.99，tan9°≈0．16，sin15.6°≈0.27，cos15.6°≈0.96，tan15.6°≈0.28，≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，BC是路边坡角为30°，长为10米的一道斜坡，在坡顶灯杆CD的顶端D处有一探射灯，射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°（图中的点A、B、C、D、M、N均在同一平面内，CM∥AN）．

    （1）求灯杆CD的高度；

    （2）求AB的长度（结果精确到0.1米）．（参考数据：=1.73．sin37°≈060，cos37°≈0.80，tan37°≈0.75）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

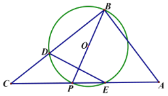
    【题目】如图中，，P是斜边AC上一个动点，以即为直径作交BC于点D，与AC的另一个交点E，连接DE．

    （1）当时，

    ①若，求的度数；

    ②求证；

    （2）当，时，

    ①是含存在点P，使得是等腰三角形，若存在求出所有符合条件的CP的长；

    ②以D为端点过P作射线DH，作点O关于DE的对称点Q恰好落在内，则CP的取值范围为________．（直接写出结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与实践

    背景阅读：旋转就是将图形上的每一点在平面内绕着旋转中心旋转固定角度的位置移动，其中“旋”是过程，“转”是结果．旋转作为图形变换的一种，具备图形旋转前后对应点到旋转中心的距离相等：对应点与旋转中心所连线段的夹角等于旋转角：旋转前、后的图形是全等图形等性质．所以充分运用这些性质是在解决有关旋转问题的关健．

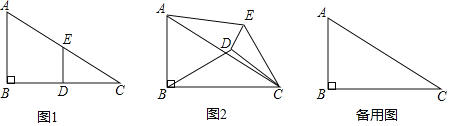
    实践操作：如图1，在Rt△ABC中，∠B＝90°，BC＝2AB＝12，点D，E分别是边BC，AC的中点，连接DE，将△EDC绕点C按顺时针方向旋转，记旋转角为α．

    问题解决：（1）①当α＝0°时，＝　 　；②当α＝180°时，＝　 　．

    （2）试判断：当0°≤a＜360°时，的大小有无变化？请仅就图2的情形给出证明．

    问题再探：（3）当△EDC旋转至A，D，E三点共线时，求得线段BD的长为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，□ABCD的对角线AC，BD相交于点O，E、F、G、H分别是OA、OB、OC、OD的中点，那么□ABCD与四边形EFGH是否是位似图形？为什么？

    查看答案和解析>>

    同步练习册答案