
 如图所示,在离水面高度为5m的岸上C点有人用绳子拉船靠岸,开始时绳子CB与水面AB的夹角为30°,此人以每秒0.5m的速度往回收绳子,8s后船被拉到了点D的位置,问船向岸边移动了多少米?
如图所示,在离水面高度为5m的岸上C点有人用绳子拉船靠岸,开始时绳子CB与水面AB的夹角为30°,此人以每秒0.5m的速度往回收绳子,8s后船被拉到了点D的位置,问船向岸边移动了多少米? 分析 首先表示出8秒后收回的绳子长,可得CD的长,在Rt△ACD中和Rt△ACB中利用勾股定理算出AD、AB的长,即可得到DB的长.
解答 解:∵AC=5m,∠CBA=30°,
∴CB=2AC=10m,
此人以每秒0.5m的速度收绳,则8秒后收回的绳子长为:0.5×8=4m,
∴CD=10-4=6(m),
在Rt△ACD中:AD=$\sqrt{C{D}^{2}-A{C}^{2}}$=$\sqrt{{6}^{2}-{5}^{2}}$=$\sqrt{11}$(m),
在Rt△ACB中:AB=$\sqrt{C{B}^{2}-A{C}^{2}}$=$\sqrt{100-25}$=5$\sqrt{3}$(m),
则BD=AB-AD=5$\sqrt{3}$-$\sqrt{11}$(m).
答:船向岸边移动了(5$\sqrt{3}$-$\sqrt{11}$)米.
点评 此题主要考查了勾股定理的应用,关键是熟练掌握勾股定理,在直角三角形中,知道任何两边都可以表示出第三边.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{75}{100}$x-20=$\frac{9}{10}$x+25 | B. | $\frac{75}{100}$x+25=$\frac{9}{10}$x-20 | ||
| C. | $\frac{75}{100}$x-25=$\frac{9}{10}$x+20 | D. | $\frac{75}{100}$x+20=$\frac{9}{10}$x+25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
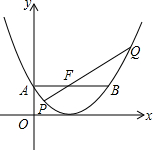 如图,已知抛物线C1:y1=$\frac{1}{4}$x2-x+1,点F(2,1).
如图,已知抛物线C1:y1=$\frac{1}{4}$x2-x+1,点F(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$-$\sqrt{2}$=3 | B. | $\frac{4}{\sqrt{2}}$=2$\sqrt{2}$ | C. | (2$\sqrt{5}$)2=10 | D. | $\sqrt{(-3)^{2}}=-3$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com