
科目:初中数学 来源: 题型:解答题
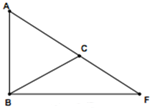 在△ABF中,C为AF上一点且AB=AC.
在△ABF中,C为AF上一点且AB=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
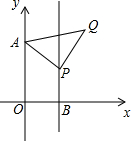 如图,已知在平面直角坐标系xOy中,O为坐标原点,A(0,5),B(3,0),过点B作直线l∥y轴,点P(3,b)是直线l上的一个动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=90°,当点P在直线l上运动时,点Q也随时之运动,问:当b=$\frac{23}{7}$时,AQ+BQ的值最小为$\sqrt{130}$.
如图,已知在平面直角坐标系xOy中,O为坐标原点,A(0,5),B(3,0),过点B作直线l∥y轴,点P(3,b)是直线l上的一个动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=90°,当点P在直线l上运动时,点Q也随时之运动,问:当b=$\frac{23}{7}$时,AQ+BQ的值最小为$\sqrt{130}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年级 | 七年级 | 八年级 | 九年级 |
| 合格人数 | 270 | 262 | 254 |
| A. | 七年级的合格率最高 | B. | 八年级的学生人数为262名 | ||
| C. | 八年级的合格率高于全校的合格率 | D. | 九年级的合格人数最少 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
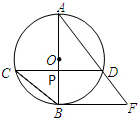 如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠ABC.
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是我们数学课本上采用的科学计算器面板,利用该型号计算器计算$\sqrt{2}$cos55°,按键顺序正确的是( )
如图,是我们数学课本上采用的科学计算器面板,利用该型号计算器计算$\sqrt{2}$cos55°,按键顺序正确的是( )| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com