
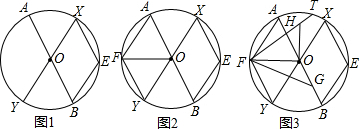
分析 (1)首先证明∠BOX=∠EOY,再根据∠EOY=2∠EXO即可证明.
(2)首先证明$\widehat{EB}$=$\widehat{EX}$,推出EB=EX,由△OEX≌△OEB,推出∠OEX=∠OEB,推出△EOX是等边三角形,由此即可解决问题.
(3)由△AFH≌△OFG,得到∠FAH=∠FOG=120°,所以点H在线段AX上,由AX∥OF,OH⊥OF,属于OH⊥AX,所以AH=HX=1,在Rt△FOH中,FH=$\sqrt{O{F}^{2}+O{H}^{2}}$=$\sqrt{{2}^{2}+(\sqrt{3})^{2}}$=$\sqrt{7}$,由FH•HT=AH•HX(相交弦定理),求出HT即可.
解答 (1)证明:如图1中,连接BX、OE.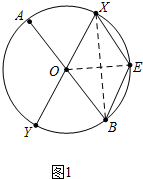
∵BE∥XY,
∴∠YXB=∠XBE,
∴$\widehat{BY}$=$\widehat{EX}$,
∴$\widehat{EY}$=$\widehat{BX}$,
∴∠EOY=∠BOX,
∵∠EOY=2∠EXO,
∴∠BOX=2∠EXO.
(2)如图2中,连接OE.
∵OF平分∠AOY,
∴$\widehat{AF}$=$\widehat{FY}$,
∵AF=BE,
∴$\widehat{AF}$=$\widehat{BE}$,
∵$\widehat{AY}$=$\widehat{BX}$,
∴$\widehat{EX}$=$\widehat{BE}$,
∴AF=FY=BE=EX,
在△OEX和△OEB中,
$\left\{\begin{array}{l}{OE=OE}\\{OX=OB}\\{EX=EB}\end{array}\right.$,
∴△OEX≌△OEB,
∴∠OEX=∠OEB,
∵BE∥XY,
∴∠EOX=∠OEB=∠XEO,
∴XO=XE=OE,
∵OA=OY=OE=OX,
∴AF=FY=OY=OA,
∴四边形AFYO是菱形.
(3)如图3中,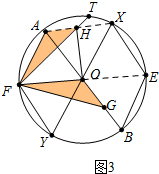
由(2)△AFO,△OEB,△OEY,△OFY都是等边三角形,
∴∠AFO=∠HFG=60°,
∴∠AFH=∠OFG,
在△AFH和△OFG中,
$\left\{\begin{array}{l}{AF=OF}\\{∠AFH=∠OFG}\\{HF=FG}\end{array}\right.$,
∴△AFH≌△OFG,
∴∠FAH=∠FOG=120°,
∴点H在线段AX上,
∵AX∥OF,OH⊥OF,
∴OH⊥AX,
∴AH=HX=1,
在Rt△FOH中,FH=$\sqrt{O{F}^{2}+O{H}^{2}}$=$\sqrt{{2}^{2}+(\sqrt{3})^{2}}$=$\sqrt{7}$.
∵FH•HT=AH•HX(相交弦定理),
∴HT=$\frac{1×1}{\sqrt{7}}$=$\frac{\sqrt{7}}{7}$.
点评 本题考查圆综合题、平行线的性质.圆心角与圆周角的关系、全等三角形的判定和性质、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,第三个问题的关键是发现△AFH≌△OFG,推出点H在线段AX上,题目的综合性比较强,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
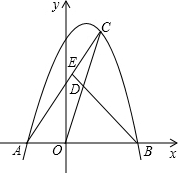 如图,抛物线y=-x2+mx+2m2(m>0)与x轴交于A,B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A,B不重合),D是OC的中点,连结BD并延长,交AC于点E,则$\frac{CE}{AE}$的值是( )
如图,抛物线y=-x2+mx+2m2(m>0)与x轴交于A,B两点,点A在点B的左边,C是抛物线上一个动点(点C与点A,B不重合),D是OC的中点,连结BD并延长,交AC于点E,则$\frac{CE}{AE}$的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 cm,2 cm,3.5 cm | B. | 4 cm,5 cm,9 cm | ||
| C. | 5 cm,8 cm,15 cm | D. | 6 cm,8 cm,9 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-b)-(a+b)=0 | B. | x-(y+1)=-(-x+y-1) | ||
| C. | 4m-n+1=4m-(n-1) | D. | 3x-2y+z=-(3x+2y-z) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 50 | B. | 60 | C. | 64 | D. | 72 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y3>y1>y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com