
分析 (1)结合题意,分别列出费用与时间的关系式,当(A)种费用比(B)种费用低时,可以找出此时x的取值范围,从而得出结论;
(2)将20与(1)中的临界点进行比较,从而决定选取那种方式,代入数据即可求出应缴费用.
解答 解:(1)令该用户平均每月的电话拨号入网为y元,
(A)种方式收费:y=(0.05+0.02)×60x;
(B)种方式收费:y=50+0.02×60x.
当(A)种收费方式≤(B)种收费方式时,有0.07×60x≤50+0.02×60x,解得x≤$\frac{50}{3}$.
故当x≤$\frac{50}{3}$时,选(A)种方式收费划算,当x>$\frac{50}{3}$时,选(B)种方式收费划算.
(2)∵20>$\frac{50}{3}$,
∴选(B)种收费方式,
此时y=50+0.02×60×20=74.
答:若x=20时,选用(B)种收费方式应缴74元钱.
点评 本题考查了一次函数的应用,解题的关键是:(1)找出两种收费方式的关系式,进行比较;(2)比较20与(1)中的临界点,从而确定选取哪种收费方式.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
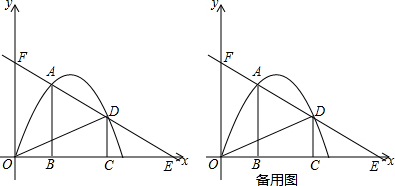
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
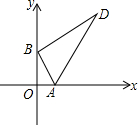 Rt△ABD的两顶点A、B分别在x轴和y轴上运动,其中∠ABD=90°,∠D=30°,AB=4,则顶点D到原点O的距离的最大值和最小值的乘积为48.
Rt△ABD的两顶点A、B分别在x轴和y轴上运动,其中∠ABD=90°,∠D=30°,AB=4,则顶点D到原点O的距离的最大值和最小值的乘积为48.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 2015年4月1日,杜桥镇开通了公共自行车出租服务,每次租车1个小时内免费,若超过1小时,将按以下标准收费:第一个小时为1元,第二个小时为2元,第三个小时及以上,按每小时3元收费,不足1小时按1小时计算,一天收取的费用最高不超过10元.如果小明上午9:00租车,当天11:40还车,那么小明应付租车费( )
2015年4月1日,杜桥镇开通了公共自行车出租服务,每次租车1个小时内免费,若超过1小时,将按以下标准收费:第一个小时为1元,第二个小时为2元,第三个小时及以上,按每小时3元收费,不足1小时按1小时计算,一天收取的费用最高不超过10元.如果小明上午9:00租车,当天11:40还车,那么小明应付租车费( )| A. | 1元 | B. | 2元 | C. | 3元 | D. | 6元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com