
【题目】已知平而直角坐标系xOy(如图),二次函数y=ax2+bx+4的图像经过A(-2,0)、
B(4,0)两点,与y轴交于点C点.
(1)求这个二次函数的解析式;
(2)如果点E在线段OC上,且∠CBE=∠ACO,求点E的坐标;
(3)点M在y轴上,且位于点C上方,点N在直线BC上,点P为上述二次函数图像的对称轴上的点,如果以C、M、N、P为顶点的四边形是菱形,求点M的坐标.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 或 M(0,6)
或 M(0,6)
【解析】分析:![]() 用待定系数法求二次函数解析式即可.
用待定系数法求二次函数解析式即可.
![]() 过点
过点![]() 作
作![]() 于点
于点![]() 在Rt△COB中,得出CH=EH.
在Rt△COB中,得出CH=EH.
在Rt△EBH中,![]() . 设
. 设![]() 则
则![]() CH=k,
CH=k,![]() .
.
列方程求解即可.
![]() 分3种情况进行讨论①当
分3种情况进行讨论①当![]() 为菱形
为菱形![]() 的边时,②当
的边时,②当![]() 为菱形
为菱形![]() 的边时,
的边时,
③当![]() 为菱形
为菱形![]() 的对角线时,分别求解即可.
的对角线时,分别求解即可.
详解:(1)∵ 抛物线![]() 与
与![]() 轴交于点A(-2,0),B(4,0),
轴交于点A(-2,0),B(4,0),
∴ ![]()
解得 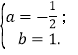
∴ 抛物线的解析式为![]()
(2)过点![]() 作
作![]() 于点
于点![]()
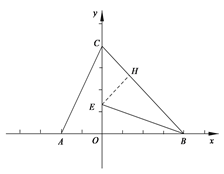
在Rt△ACO中, ∵A(-2,0),∴ OA=2,
当![]() 时
时 ![]() ∴OC=4,
∴OC=4,
在Rt△COB中,∵∠COB=90°,OC=OB=4,
∴![]() .
.
∵![]() ,∴CH=EH.
,∴CH=EH.
∴在Rt△ACO中,![]() ,
,
∵∠CBE=∠ACO,∴在Rt△EBH中,![]() .
.
设![]() 则
则![]() CH=k,
CH=k,![]() .
.
∴![]() .
.
∴![]()
∴![]()
∴![]() ∴
∴![]()
(3)∵ ![]()
∴抛物线的对称轴为直线![]()
①当![]() 为菱形
为菱形![]() 的边时,
的边时,
∴![]()
![]()
∵点P在二次函数的对称轴上,
点![]() 的横坐标为1,点
的横坐标为1,点![]() 的横坐标为1,
的横坐标为1,
∴![]() .
.
∵四边形![]() 是菱形,∴
是菱形,∴![]()
∴![]()
∴![]() .
.
②当![]() 为菱形
为菱形![]() 的边时,不存在,
的边时,不存在,
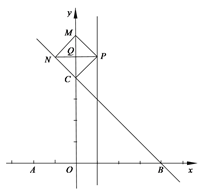
③当![]() 为菱形
为菱形![]() 的对角线时,
的对角线时,
设![]() 交
交![]() 于点
于点![]()
∴![]() 互相垂直平分,
互相垂直平分,
∴![]() .
.![]()
∵点![]() 在直线
在直线![]() 上,
上,![]()
在![]() 中,
中,![]()
∴![]() ∴
∴![]()
∴![]() ∴
∴![]()
∴ ![]()
∴综上所述![]() 或 M(0,6).
或 M(0,6).


科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx﹣4的图象开口向上,与x轴的交点为(4,0)、(﹣2,0),则当x1=﹣1,x2=2时,对应的函数值y1和y2的大小关系为( )
A. y1>y2 B. y1=y2 C. y1<y2 D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①
cos(α+β)=cosαcosβ﹣sinαsinβ②
tan(α+β)=![]() ③
③
利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,如:
tan105°=tan(45°+60°)=![]() =﹣(2+
=﹣(2+![]() ).
).
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
如图,直升飞机在一建筑物CD上方A点处测得建筑物顶端D点的俯角α=60°,底端C点的俯角β=75°,此时直升飞机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
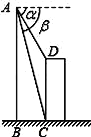
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①若|a|=﹣b,|b|=b,则a=b=0;②若﹣a不是正数,则a为非负数;③|﹣a2|=(﹣a)2;④若![]() ,则
,则![]() ;⑤平面内n条直线两两相交,最多
;⑤平面内n条直线两两相交,最多![]() 个交点.其中正确的结论有( )
个交点.其中正确的结论有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
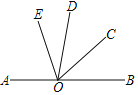
【题目】如图,点O在直线AB上,∠AOC与∠COD互补,OE平分∠AOC.
(1)若∠BOC=40°,则∠DOE的度数为 ;
(2)若∠DOE=48°,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是( )
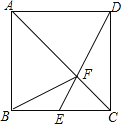
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若a+b=ab,则称a、b是“相伴数”,例如:3+1.5=3×1.5,因此3和1.5是一组“相伴数”
(1)﹣1与 是一组“相伴数”;
(2)若m、n是一组“相伴数”,2mn﹣![]() [3m+2(
[3m+2(![]() n﹣m)+3mn﹣6]的值.
n﹣m)+3mn﹣6]的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com