
����Ŀ����1�����ⷢ��
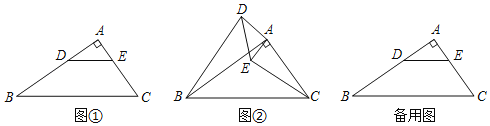
��ͼ�٣���Rt��ABC�У���A��90����AB��kAC����D��AB��һ�㣬DE��BC��
��գ�BD��CE��������ϵΪ�� ����λ�ù�ϵΪ�� ����
��2�����̽��
��ͼ�ڣ�����ADE���ŵ�A˳ʱ����ת����ת��Ϊ����0��������90����������BD��CE�����ʣ�1���еĽ��ۻ��������������������֤����������������˵�����ɣ�
��3����չ����
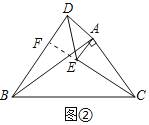
�ڣ�2���������£�����ADE�Ƶ�A˳ʱ����ת����ת��Ϊ����ֱ��BD��CE���ڵ�F����AC��1��AB��![]() ������ACE��15��ʱ����ֱ��д��BF�ij���
������ACE��15��ʱ����ֱ��д��BF�ij���
���𰸡���1�����ⷢ�֣�BD��kCE��BD��CE����2�����̽������1���еĽ��ۻ����������ɼ���������3����չ���죺BF�ij�Ϊ![]() ��
��![]() ��
��
��������
��1����ƽ���߷��߶γɱ����ɵ�![]() ������֪�������ɵ�BD=kEC���ɡ�A=90�����ɵó�BD��CE��
������֪�������ɵ�BD=kEC���ɡ�A=90�����ɵó�BD��CE��
��2��ͨ��֤����ABD�ס�ACE���ɵ�![]() =k�����ɵ�BD=kEC����֤����BFC=90�������ɵó�BD��CE��
=k�����ɵ�BD=kEC����֤����BFC=90�������ɵó�BD��CE��
��3��������������ۣ������������ε����ʿɵá�ACE=��ABD������֤��BFC=90������ֱ�������ε����ʺ��ɶ�������BF��ֵ��
��1�����ⷢ�֣�
�⣺��DE��BC��
��![]() ��
��![]() ��
��
��AB��kAC��
��BD��kCE��
�ߡ�A��90����
��AB��AC��
��BD��CE��
�ʴ�Ϊ��BD��kCE��BD��CE��
��2�����̽����
�⣺��1���еĽ��ۻ��������������£�
�ӳ�CE��BD��F����ͼ����ʾ��
����ת�����ʿ�֪����BAD����CAE��
��DE��BC��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
���ABD�ס�ACE��
��![]() ��
��![]() ��k����ABD����ACE��
��k����ABD����ACE��
��BD��kEC��
�ߡ�CBF+��BCF����ABD+��ABC+��BCF����ACE+��BCF+��ABC����ACB+��ABC��90����
���BFC��90����
��BD��CE��
��3����չ���죺
�⣺����ת�����ʿ�֪����BAD����CAE
��![]() ��
��![]() ��
��
���ABD�ס�ACE��
���ACE��15������ABD��
�ߡ�ABC+��ACB��90����
���FBC+��FCB��90����
���BFC��90����
�ߡ�BAC��90����![]() ��
��
��tan��ABC��![]() ��
��
���ABC��30����
���ACB��60����
�����������
��0��������90��ʱ����ͼ����ʾ��
����Rt��BAC����ABC��30����AC��1��
��BC��2AC��2��
����Rt��BFC����CBF��30��+15����45����BC��2��
��BF��CF��![]() ��
��
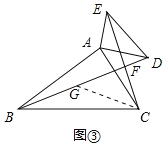
������90��ʱ����ͼ����ʾ��
��CF��a����BF��ȡ��G��ʹ��BCG��15��
�ߡ�BCF��60��+15����75������CBF����ABC����ABD��30����15����15����
���CFB��90����
���GCF��60������CBF����BCG��
��CG��BG��2a��GF��![]() a��
a��
��BF��BG+GF����2+![]() ��a��
��a��
��CF2+BF2��BC2
��a2+��2a+![]() a�� 2��22��
a�� 2��22��
��ã�a2��2��![]() ��
��
��a��![]() ��
��
��BF����2+![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
����BF�ij�Ϊ![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
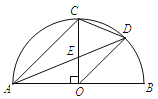
����Ŀ����ͼ��AB�ǰ�ԲOֱ�����뾶OC��AB������AC����CAB��ƽ����AD�ֱ�OC�ڵ�E����![]() �ڵ�D������CD��OD�������������ۣ���AC��OD����AC��2CD�����߶�CD��CE��CO�ı����������������ȷ���۵�����ǣ� ��
�ڵ�D������CD��OD�������������ۣ���AC��OD����AC��2CD�����߶�CD��CE��CO�ı����������������ȷ���۵�����ǣ� ��
A.�٢�B.�ڢ�
C.�٢�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
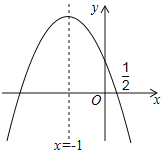
����Ŀ����ͼ��������y��ax2+bx+c�ĶԳ�����x����1���ҹ��㣨![]() ��0���������н��ۣ���abc��0����a��2b+4c��0����25a+4c��10b����3b+2c��0����a��b��m��am��b�����������д���Ľ����У�����������
��0���������н��ۣ���abc��0����a��2b+4c��0����25a+4c��10b����3b+2c��0����a��b��m��am��b�����������д���Ľ����У�����������
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
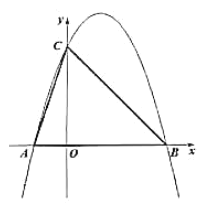
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ABC��������������ֱ�ΪA��1��1����B��4��0����C��4��4����
��1��������Ҫ����ͼ��
�ٽ���ABC����ƽ��4����λ���õ���A1B1C1��
�ڽ���A1B1C1�Ƶ�B1��ʱ����ת90�㣬�õ���A2B2C2��
��2�����C1����ת��������������·������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й�ʫ�ʴ�ᡷ�������л�ʫ�ʣ�Ѱ�Ļ�����Ʒ����֮����Ϊ������ּ������ͨ����ʫ��֪ʶ�ı�ƴ������������ȫ��������Щ����ѧ���Ĺ�ʫ�ʣ�����ʫ��֮��������ʫ��֮Ȥ���ӹ��˵��ǻۺ��黳�м�ȡӪ�����������飬�Կ����������ܹ��ʦ����ϲ����ij��ѧΪ�˽�ѧУѧ����ʫ��ˮƽ���Ӱˡ����꼶�������ȡ��20��ѧ�������˲��ԣ������ˡ����꼶���Գɼ����ٷ��ƣ���λ���֣��������£�
�ռ�����
���꼶 93 92 84 55 85 82 66 74 88 67 87 87 67 61 87 61 78 57 72 75
���꼶 68 66 79 92 86 87 61 86 90 83 90 78 70 67 53 79 86 71 61 89
�������ݰ����·������������ݣ�����ȫ����
���Գɼ�x���֣� | 50��x��60 | 60��x��70 | 70��x��80 | 80��x��90 | 90��x��100 |
�� | 2 | 4 | |||
�� | 1 | 5 | 5 | 6 | 3 |
˵�������Գɼ�x���֣�������x��80Ϊ���㣬70��x��80Ϊ���ã�60��x��70Ϊ�ϸ�0��x��60Ϊ���ϸ�
�������ݲ�ȫ���б����е�ͳ������
�꼶 | ƽ���� | ��λ�� | ���� |
�� | 75.9 | 76.5 | |
�� | 77.1 | 79 | 86 |
����
��1���ڴ˴β����У���λͬѧ�ijɼ���78span>�֣��������ڵ��꼶�����е�ƫ�ϣ�����λͬѧ�����ĸ��꼶��
��2�������꼶��800��ѧ�������ƾ��꼶ʫ��ˮƽ�ﵽ�����ѧ���ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ⷽ�̣�x2��1��2��5��x2��1��+4=0�����ǿ��Խ�x2��1��Ϊһ�����壬Ȼ����x2��1=y����
��x2��1��=y2��ԭ���̻�Ϊy2��5y+4=0����
���y1=1��y2=4
��y=1ʱ��x2��1=1����x2=2����x=��![]() ��
��
��y=4ʱ��x2��1=4����x2=5����x=��![]() ��
��
��ԭ���̵Ľ�Ϊx1=![]() ��x2=��
��x2=��![]() ��x3=
��x3=![]() ��x4=��
��x4=��![]()
������⣺
��1����գ�����ԭ���̵õ����̢ٵĹ����У������� �����ﵽ�˽��ε�Ŀ�ģ��������� ������ѧ˼�룮
��2���ⷽ�̣�x4��x2��6=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�������
��������![]() ��
��![]() �����������ֱ�Ϊ
�����������ֱ�Ϊ![]() ��
��![]() ����
����![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ��
��
��1���������ߵı���ʽ��
��2������![]() ��
��![]() ����
����![]() ������ֵ��
������ֵ��
��3����![]() ���������ϣ���
���������ϣ���![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���ÿ��![]() Ԫ�ļ۸�һ����Ʒ�������з���������Ʒÿ���������
Ԫ�ļ۸�һ����Ʒ�������з���������Ʒÿ���������![]() ��������ÿ�������ۼ�
��������ÿ�������ۼ�![]() ��Ԫ������һ�κ�����ϵ
��Ԫ������һ�κ�����ϵ![]() .
.
��1�����̳�����������Ʒÿ�����������![]() ��Ԫ����ÿ�����ۼ�
��Ԫ����ÿ�����ۼ�![]() ��Ԫ��֮��ĺ�����ϵʽ.
��Ԫ��֮��ĺ�����ϵʽ.
��2���̳�ÿ������������Ʒ�����������ܷ�ﵽ![]() Ԫ������ܣ������ʱ�����ۼ۸�������ܣ�˵������.
Ԫ������ܣ������ʱ�����ۼ۸�������ܣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
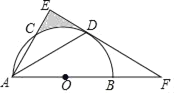
����Ŀ����ͼ��ABΪ��ԲO��ֱ����AC�ǡ�O��һ���ң�DΪ![]() ���е㣬��DE��AC����AB���ӳ����ڵ�F������DA��
���е㣬��DE��AC����AB���ӳ����ڵ�F������DA��
��1����֤��EFΪ��ԲO�����ߣ�
��2����DA��DF��6![]() ������Ӱ����������������������źͦУ�
������Ӱ����������������������źͦУ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com