
【题目】如图,已知AM∥BN,∠B=40°,点P是BN上一动点(与点B不重合).AC、AD分别平分∠BAP和∠PAM,交射线BN于点C、D.

(1)求∠CAD的度数;
(2)当点P运动到当∠ACB=∠BAD时,求∠BAC的度数.
【答案】(1)∠CAD=70°;(2)=35°
【解析】
(1)由平行线的性质,角平分线的定义,角的和差求得∠CAD的度数为70°;
(2)由平行线的性质,角平分线的定义,已知等量关系求得∠BAC的度数为35°.
如图所示:
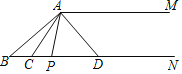
(1)∵AM∥BN,
∴∠B+∠BAM=180°,
又∵∠B=40°,
∴∠BAM=180°﹣∠B=140°,
又∵AC、AD分别平分∠BAP和∠PAM,
∴∠CAP=![]() ∠BAP,∠PAD=
∠BAP,∠PAD=![]() ∠PAM,
∠PAM,
∴∠CAP+∠PAD=![]() (∠BAP+∠PAM)
(∠BAP+∠PAM)
=![]() ∠BAM
∠BAM
=![]()
=70°
又∵∠CAD=∠CAP+∠PAD,
∴∠CAD=70°;
(2)∵AM∥BN,
∴∠ACB=∠MAC,
又∵∠ACB=∠BAD,
∴∠MAC=∠BAD,
∴∠MAC﹣∠DAC=∠BAD﹣∠DAC,
∴∠MAD=∠BAC
又∵AC,AD分别平分∠BAP和∠PAM,
∴∠BAC=∠CAP,∠MAD=∠PAD
∴∠BAC=∠CAP=∠MAD=∠PAD
又∵∠BAM=140°
∴∠BAC=![]() ∠BAM=
∠BAM=![]() ×140°=35°.
×140°=35°.


科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有4个小球,分别标有数字1,2,3,4;这些小球除所标数字不同外,其余完全相同,甲乙两人每次同时从袋中各随机摸出一个小球,记下球上的数字,并计算它们的积.
![]() 请用画树状图或列表的方法,求两数积是8的概率;
请用画树状图或列表的方法,求两数积是8的概率;
![]() 甲乙两人想用这种方式做游戏,他们规定,当两数之积是偶数时,甲得1分,当两数之积是奇数时,乙得3分,你认为这个游戏公平吗?请说明理由,若你认为不公平,请修改得分规则,使游戏公平.
甲乙两人想用这种方式做游戏,他们规定,当两数之积是偶数时,甲得1分,当两数之积是奇数时,乙得3分,你认为这个游戏公平吗?请说明理由,若你认为不公平,请修改得分规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
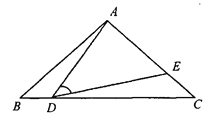
【题目】如图,在△ABC中,AB=AC=9,BC=12,∠B=∠C,点D从B出发以每秒2厘米的速度在线段BC上从B向C方向运动,点E同时从C出发以每秒2厘米的速度在线段AC上从C向A运动,连接AD、DE.
(1)运动 秒时,AE=![]() DC(不必说明理由)
DC(不必说明理由)
(2)运动多少秒时,∠ADE=90°-![]() ∠BAC,并请说明理由;
∠BAC,并请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=36cm,OB=12cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外研究小组为了解学生参加课外体育活动的情况,采取抽样调查的方法从篮球、排球、乒乓球、足球及其他等五个方面调查了若干名同学的兴趣爱好![]() 每人只能选其中一项
每人只能选其中一项![]() ,并将调查结果绘制成统计图,请根据图中提供的信息解答下列问题:
,并将调查结果绘制成统计图,请根据图中提供的信息解答下列问题:
![]() 在这次考察中一共调查了______名学生,请补全条形统计图;
在这次考察中一共调查了______名学生,请补全条形统计图;
![]() 被调查同学中恰好有4名学来自初一2班,其中有2名同学选择了篮球,有2名同学选择了乒乓球,曹老师打算从这4名同学中选择两同学了解他们对体育社团的看法,请用列表法或画树状图法,求选出的两人恰好都选择同一种球的概率.
被调查同学中恰好有4名学来自初一2班,其中有2名同学选择了篮球,有2名同学选择了乒乓球,曹老师打算从这4名同学中选择两同学了解他们对体育社团的看法,请用列表法或画树状图法,求选出的两人恰好都选择同一种球的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市欲购进一种今年新上市的产品,购进价为20元![]() 件,为了调查这种新产品的销路,该超市进行了试销售,得知该产品每天的销售量
件,为了调查这种新产品的销路,该超市进行了试销售,得知该产品每天的销售量![]() 件
件![]() 与每件的销售价
与每件的销售价![]() 元
元![]() 件
件![]() 之间有如下关系:
之间有如下关系:![]()
![]() 请写出该超市销售这种产品每天的销售利润
请写出该超市销售这种产品每天的销售利润![]() 元
元![]() 与x之间的函数关系式,并求出超市能获取的最大利润是多少元.
与x之间的函数关系式,并求出超市能获取的最大利润是多少元.
![]() 若超市想获取1500元的利润
若超市想获取1500元的利润![]() 求每件的销售价.
求每件的销售价.
![]() 若超市想获取的利润不低于1500元,请求出每件的销售价X的范围?
若超市想获取的利润不低于1500元,请求出每件的销售价X的范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
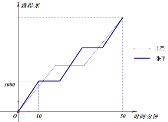
【题目】“绿带城中挂,人在画中游”,张平和王亮同学周末相约骑行于“步移景异,心旷神怡”的温江田园绿道,他们从同一地方同时骑自行车出发(骑行过程中速度保持不变),最后同时到达了同一个地方. 如图刻画了他们离出发点的路程(单位:米)与出发后的时间(单位:分钟)之间的关系. 已知张平中途两次休息时间相同,三段骑行时间也分别相同;王亮中途休息一次,两段骑行时间相同. 张平总的休息时间比王亮的休息时间多![]() 分钟. 请结合图中信息解答下列问题:
分钟. 请结合图中信息解答下列问题:
(1)在这次骑行活动中,他们的骑行路程都是多少米?
(2)求出张平和王亮的骑行速度分别是多少米/分钟?
(3)求出王亮出发后第一次追上张平的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知两条直线AB,CD被直线EF所截,分别交于点E,点F,EM平分∠AEF交CD于点M,且∠FEM=∠FME.

(1)直线AB与直线CD是否平行,说明你的理由;
(2)如图2,点G是射线MD上一动点(不与点M,F重合),EH平分∠FEG交CD于点H,过点H作HN⊥EM于点N,设∠EHN=α,∠EGF=β.
①当点G在点F的右侧时,若β=60°,求α的度数;
②当点G在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是该型号电风扇近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
![]() 求A、B两种型号的电风扇的销售单价;
求A、B两种型号的电风扇的销售单价;
![]() 若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?
若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com