
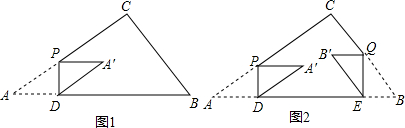
ЗжЮі ЃЈ1ЃЉРћгУШёНЧШ§НЧКЏЪ§ЕФвтвхжБНгЧѓГіЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉМЦЫуПЩЕУЃЌЗжСНжжЧщПігУШёНЧШ§НЧКЏЪ§ЕФвтвхЧѓНтЃКЂйЕБ0ЃМxЁм$\frac{40}{41}$ЪБЃЌy=12xЃЌЕБ$\frac{40}{41}$ЃМxЁм$\frac{8}{5}$ЪБЃЌy=12-$\frac{3}{10}$xЃЛ
ЃЈ3ЃЉЂйевГіЗжНчЕуЂёЁЂAЁфИеКУЕНДяBЁфEБпЪБЃЌЂђЁЂAЁфЕНEQБпгыNжиКЯЃЌРћгУЭЌвЛЬѕЯпЖЮСНжжЫуЗЈЧѓГіxжЕЃЌМДПЩЃЛЂкРћгУШёНЧШ§НЧКЏЪ§жЕгУСНжжЫуЗЈСаГіЗНГЬЧѓНтМДПЩЃЎ
НтД№ НтЃКЃЈ1ЃЉШчЭМ1ЃЌ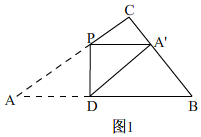
ЁпЁЯC=90ЁуЃЌAC=8РхУзЃЌBC=6РхУзЃЌ
ЁрAB=10ЃЌ
ЁрcosA=$\frac{4}{5}$ЃЌsinA=$\frac{3}{5}$ЃЌtanA=$\frac{3}{4}$ЃЌ
ЩшAP=5xЃЌ
ЁрPAЁф=AD=APcosЁЯA=$\frac{4}{5}$ЁС5x=4xЃЌCP=8-5xЃЌ
ЁрcosЁЯCPAЁф=cosЁЯA=$\frac{CP}{PAЁф}$=$\frac{8-5x}{4x}$=$\frac{4}{5}$ЃЌ
Ёрx=$\frac{40}{41}$ЃЌ
ЃЈ2ЃЉЂйЕБ0ЃМxЁм$\frac{40}{41}$ЃЌШчЭМ2ЃЌ
ЁрPAЁф=AD=APcosA=3xЃЌ
ЁрAЁфD=AP=5xЃЌ
Ёрy=4x+3x+5x=12xЃЌ
ЂкЕБ$\frac{40}{41}$ЃМxЁм$\frac{8}{5}$ЪБЃЌШчЭМ3
ЁрPE=$\frac{PC}{cosA}$=$\frac{80-50x}{8}$ЃЌ
DF=DBЁСcosA=8-$\frac{16}{5}$xЃЌ
Ёрy=3x+$\frac{80-50x}{8}$+8-$\frac{16}{5}$x+$\frac{123}{20}$x-6=12-$\frac{3}{10}$xЃЌ
МДЃКЕБ0ЃМxЁм$\frac{40}{41}$ЪБЃЌy=12xЃЌЕБ$\frac{40}{41}$ЃМxЁм$\frac{8}{5}$ЪБЃЌy=12-$\frac{3}{10}$xЃЛ
ЃЈ3ЃЉЂйЭЌЃЈ1ЃЉвЛбљгаЃЌsinB=$\frac{4}{5}$ЃЌcosB=$\frac{3}{5}$ЃЌtanB=$\frac{4}{3}$ЃЌ
ЂёЁЂAЁфИеКУЕНДяBЁфEБпЪБЃЌШчЭМ4ЃЌ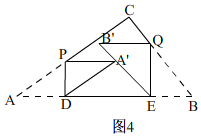
ЁрPN=$\frac{PC}{cosA}$=$\frac{80-50x}{8}$ЃЌPAЁф=4xЃЌANЁф=EB=3xЃЌPN=PAЁф+AЁфNЃЌ
Ёр$\frac{80-50x}{8}$=7xЃЌ
Ёрx=$\frac{40}{53}$ЃЌ
ЂђЁЂAЁфЕНEQБпгыБпBCНЛгкNЃЌШчЭМ5ЃЌ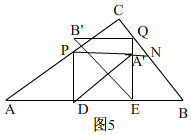
ЁрAЁфN=$\frac{QAЁф}{tanB}$=$\frac{QE-PD}{tanB}$=$\frac{3}{4}$xЃЌPN=PAЁф+AЁфN=$\frac{80-50x}{8}$ЃЌ
Ёр4x+$\frac{3}{4}$x=$\frac{80-50x}{8}$ЃЌ
Ёрx=$\frac{10}{11}$ЃЌ
Ёр$\frac{40}{53}$ЃМxЃМ$\frac{10}{11}$ЃЌ
ЂкЂёЁЂЕБAЁфBЁфЁЭABЪБЃЌШчЭМ6ЃЌ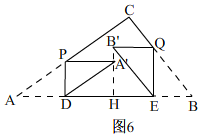
ЁрDH=PA'=ADЃЌHE=BЁфQ=EBЃЌ
ЁпAB=2AD+2EB=2ЁС4x+2ЁС3x=10ЃЌ
Ёрx=$\frac{5}{7}$ЃЌ
ЁрAЁфBЁф=QE-PD=x=$\frac{5}{7}$
ЂђЁЂЕБAЁфBЁфЁЭBCЪБЃЌШчЭМ7ЃЌ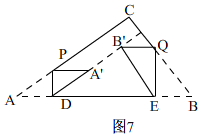
ЁрBЁфE=5xЃЌDE=10-7xЃЌ
ЁрcosB=$\frac{5x}{10-7x}$=$\frac{3}{5}$ЃЌ
Ёрx=$\frac{15}{23}$ЃЌ
ЁрAЁфBЁф=BЁфD-AЁфD=$\frac{25}{23}$ЃЌ
ЂѓЁЂЕБAЁфBЁфЁЭACЪБЃЌШчЭМ8ЃЌ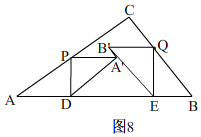
гЩЃЈ1ЃЉгаЃЌx=$\frac{40}{53}$ЃЌ
ЁрAЁфBЁф=PAЁфsinA=$\frac{50}{53}$ЃЌ
ЂєЁЂЕБQЃЌPЖМЕНДяCКѓЃЌAЁфBЁфЁЮABЧвAB=AЁфBЁф=10ЃЎШчЭМ9ЃЌ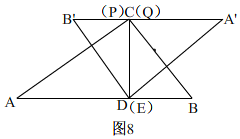
ЕуЦР ДЫЬтЪЧМИКЮБфЛЛзлКЯЬтЃЌжївЊПМВщСЫШёНЧШ§НЧКЏЪ§ЕФвтвхЃЌЗжРрЬжТлЃЌНтБОЬтЕФЙиМќЪЧвЊЗжРрвЊЗжзМЃЌФбЕуЪЧЗжРрЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
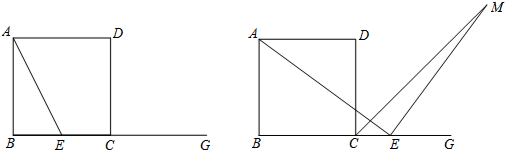
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
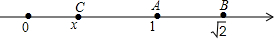 ШчЭМЃЌЪ§жсЩЯБэЪОЪ§1ЁЂ$\sqrt{2}$ЕФЖдгІЕуЗжБ№ЮЊAЁЂBЃЌЕуBЙигкЕуAЕФЖдГЦЕуЮЊCЃЌЩшЕуCЫљБэЪОЕФЪ§ЮЊxЃЌЧѓx2-2$\sqrt{2}$x+2ЕФжЕЃЎ
ШчЭМЃЌЪ§жсЩЯБэЪОЪ§1ЁЂ$\sqrt{2}$ЕФЖдгІЕуЗжБ№ЮЊAЁЂBЃЌЕуBЙигкЕуAЕФЖдГЦЕуЮЊCЃЌЩшЕуCЫљБэЪОЕФЪ§ЮЊxЃЌЧѓx2-2$\sqrt{2}$x+2ЕФжЕЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
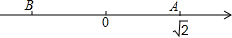 ШчЭМЃЌЪ§жсЩЯЕуAБэЪО$\sqrt{2}$ЃЌЕуBЙигкдЕуЕФЖдГЦЕуЮЊAЃЌЩшЕуBЫљБэЪОЕФЪ§ЮЊxЃЌЧѓ$\frac{1}{2}$x+$\sqrt{2}$x+$\frac{\sqrt{2}}{2}$ЕФжЕЃЎ
ШчЭМЃЌЪ§жсЩЯЕуAБэЪО$\sqrt{2}$ЃЌЕуBЙигкдЕуЕФЖдГЦЕуЮЊAЃЌЩшЕуBЫљБэЪОЕФЪ§ЮЊxЃЌЧѓ$\frac{1}{2}$x+$\sqrt{2}$x+$\frac{\sqrt{2}}{2}$ЕФжЕЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 4x2+1 | BЃЎ | 1-4x2 | CЃЎ | 4x2-1 | DЃЎ | -4x2-1 |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com