
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)探究:上述操作能验证的等式是 ;(请选择正确的一个)

A.a2-2ab+b2=(a-b)2 B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
(2)应用:利用你从(1)选出的等式,完成下列各题:
①已知9x2-4y2=24,3x+2y=6,求3x-2y的值;
②计算:![]()
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,将正方形纸片ABCD沿FH折叠,使点D与AB的中点E重合,则△FAE与△EBG的面积之比为( ) 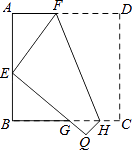
A.4:9
B.2:3
C.3:4
D.9:16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0),过A作AA1⊥OB,垂足为点A1;过点A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;则A2A3=;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的纵坐标为 . 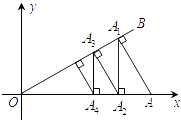
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC沿射线BC方向平移得到△DEF,已知AB=16cm,BE=10cm,DH=6cm,则图中阴影部分的面积为__________.
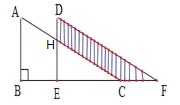
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实现区域教育均衡发展,我市计划对某县A、B两类薄弱学校全部进行改造,根据预算,共需资金1575万元,改造一所A类学校和两所B类学校共需资金230万元;改造两所A类学校和一所B类学校共需资金205万元.
(1)改造一所A类学校和一所B类学校所需的资金分别是多少万元?
(2)我市计划今年对该县A、B两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担。若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到A、B两类学校的改造资金分别为每所10万元和15万元。请你通过计算求出有几种改造方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.
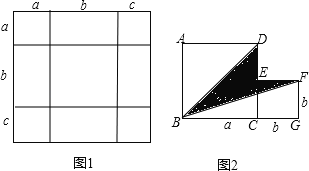
(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.
(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
∵∠1=∠2,∠2=∠3 ,∠1=∠4( )
∴∠3=∠4( )
∴________∥_______ ( )
∴∠C=∠ABD( )
∵∠C=∠D( )
∴∠D=∠ABD( )
∴DF∥AC( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com