
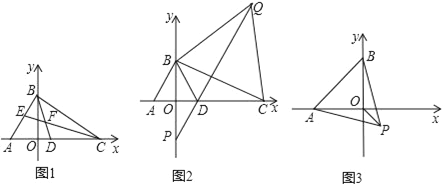
【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=![]() DC?请求出点C的坐标;
DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
【答案】(1)6;(2)C的坐标为(12,0);(3)![]() .
.
【解析】
(1)作∠DCH=10°,CH 交 BD 的延长线于 H,分别证明△OBD≌△HCD 和△AOB≌△FHC,根据全等三角形的对应边相等解答;
(2)证明△CBA≌△QBD,根据全等三角形的性质得到∠BDQ=∠BAC=60°,求出 CD,得到答案;
(3)以 OA 为对称轴作等边△ADE,连接 EP,并延长 EP 交 x 轴于点 F.证明点 P 在直线 EF 上运动,根据垂线段最短解答.
解:(1)作∠DCH=10°,CH 交 BD 的延长线于 H,
∵∠BAO=60°,
∴∠ABO=30°,
∴AB=2OA=6,
∵∠BAO=60°,∠BCO=40°,
∴∠ABC=180°﹣60°﹣40°=80°,
∵BD 是△ABC 的角平分线,
∴∠ABD=∠CBD=40°,
∴∠CBD=∠DCB,∠OBD=40°﹣30°=10°,
∴DB=DC,
在△OBD 和△HCD 中,
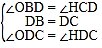
∴△OBD≌△HCD(ASA),
∴OB=HC,
在△AOB 和△FHC 中,
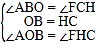
∴△AOB≌△FHC(ASA),
∴CF=AB=6,
故答案为6;
(2)∵△ABD 和△BCQ 是等边三角形,
∴∠ABD=∠CBQ=60°,
∴∠ABC=∠DBQ,
在△CBA 和△QBD 中,
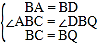
∴△CBA≌△QBD(SAS),
∴∠BDQ=∠BAC=60°,
∴∠PDO=60°,
∴PD=2DO=6,
∵PD=![]() DC,
DC,
∴DC=9,即 OC=OD+CD=12,
∴点 C的坐标为(12,0);
(3)如图3,以 OA为对称轴作等边△ADE,连接 EP,并延长 EP交 x 轴于点F.
由(2)得,△AEP≌△ADB,
∴∠AEP=∠ADB=120°,
∴∠OEF=60°,
∴OF=OA=3,
∴点P在直线 EF上运动,当 OP⊥EF时,OP最小,
∴OP=![]() OF=
OF=![]()
则OP的最小值为![]() .
.


科目:初中数学 来源: 题型:
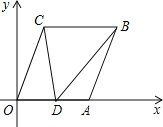
【题目】如图,已知A(6,0),B(8,5),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)求对角线AC的长;
(2)设点D的坐标为(x,0),△ODC与△ABD的面积分别记为S1,S2.设S=S1﹣S2,写出S关于x的函数解析式,并探究是否存在点D使S与△DBC的面积相等?如果存在,用坐标形式写出点D的位置;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
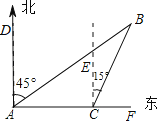
【题目】如图,一艘游轮在A处测得北偏东45°的方向上有一灯塔B.游轮以20![]() 海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:
海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表三行数的规律,回答下列问题:
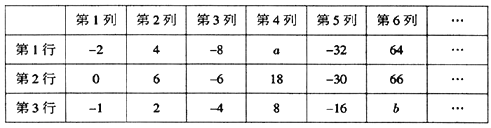
(1)第1行的第四个数a是多少;第3行的第六个数b是多少;
(2)若第1行的某一列的数为c,则第2行与它同一列的数为多少;
(3)巳知第n列的三个数的和为2562,若设第1行第n列的数为x,试求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
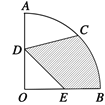
【题目】如图,在圆心角为 ![]() 的扇形
的扇形 ![]() 中,半径
中,半径 ![]() =4cm,
=4cm,![]() 为弧
为弧 ![]() 的中点,
的中点,![]() ,
,![]() 分别是
分别是 ![]() ,
,![]() 的中点,则图中阴影部分的面积(单位
的中点,则图中阴影部分的面积(单位![]() )为( )
)为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分别直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
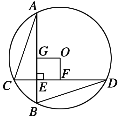
【题目】如图,⊙O的半径为5,弦AB⊥CD于E,AB=CD=8.
(1)求证:AC=BD;
(2)若OF⊥CD于F,OG⊥AB于G,试说明四边形OFEG是正方形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
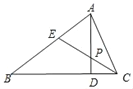
【题目】如图,在△ABC中,AD是△ABC的高线,CE是△ABC的角平分线,它们相交于点P.
(1)若∠B=40°,∠AEC=75°,求证:AB=BC;
(2)若∠BAC=90°,AP为△AEC边EC上中线,求∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com