
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )

A. ![]() B. 3 C. 1 D.
B. 3 C. 1 D. ![]()
【答案】A
【解析】首先利用勾股定理计算出AC的长,再根据折叠可得△DEC≌△D′EC,设ED=x,则D′E=x,AD′=AC﹣CD′=2,AE=4﹣x,再根据勾股定理可得方程22+x2=(4﹣x)2,再解方程即可.
解:∵AB=3,AD=4,
∴DC=3,
∴AC=![]() =5,
=5,
根据折叠可得:△DEC≌△D′EC,
∴D′C=DC=3,DE=D′E,
设ED=x,则D′E=x,AD′=AC﹣CD′=2,AE=4﹣x,
在Rt△AED′中:(AD′)2+(ED′)2=AE2,
22+x2=(4﹣x)2,
解得:x=![]() ,
,
故选:A.
“点睛”此题主要考查了图形的翻着变换,以及勾股定理的应用,关键是掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


科目:初中数学 来源: 题型:
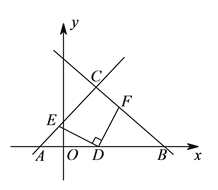
【题目】如图,在平面直角坐标系中,已知直线![]() 和
和![]() 与
与![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() ,设两直线相交于点
,设两直线相交于点![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上一个动点(不与点
上一个动点(不与点![]() 和
和![]() 重合),连结
重合),连结![]() ,并过点
,并过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(![]() )判断
)判断![]() 的形状,并说明理由.
的形状,并说明理由.
(![]() )当点
)当点![]() 在线段
在线段![]() 上运动时,四边形
上运动时,四边形![]() 的面积是否为定值?若是,请求出这个定值;若不是,请说明理由.
的面积是否为定值?若是,请求出这个定值;若不是,请说明理由.
(![]() )当点
)当点![]() 的横坐标为
的横坐标为![]() 时,在
时,在![]() 轴上找到一点
轴上找到一点![]() 使得
使得![]() 的周长最小,请直接写出点
的周长最小,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数的图象经过P(-2·3).
(1)求此反比例函数的解析式;
(2)点A(2.-3)、B(3,2)是否在这个函数的图象上?
(3)这个函数的图象位于哪些象限?函数值y随自变量x的减小如何变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题:
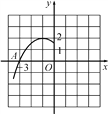
(1)抛物线与x轴的一个交点A的坐标是 ,则抛物线与x轴的另一个交点B的坐标是 ;
(2)确定a的值;
(3)设抛物线的顶点是P,试求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
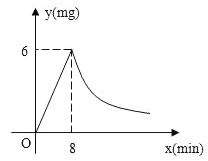
【题目】为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,学生方可进教室,那么从消毒开始,至少需要几分钟后,学生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(![]() )求抛物线的解析式.
)求抛物线的解析式.
(![]() )设抛物线的顶点为
)设抛物线的顶点为![]() ,点
,点![]() 在抛物线的对称轴上,且
在抛物线的对称轴上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(![]() )点
)点![]() 在直线
在直线![]() 上方的抛物线上,是否存在点
上方的抛物线上,是否存在点![]() 使
使![]() 的面积最大,若存在,请求出点
的面积最大,若存在,请求出点![]() 坐标.
坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com