
【题目】深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
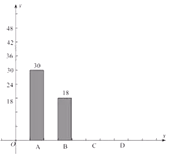
类型 | 频数 | 频率 |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
(1)学生共________人, ![]() ________,
________, ![]() ________;
________;
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有________人.
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】探究与发现:如图1所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:

(1)观察“规形图”,试探究![]() 与
与![]() 之间的关系,并说明理由;
之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在![]() 上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若
上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若![]() ,则
,则![]() ________;
________;
②如图3,DC平分![]() ,EC平分
,EC平分![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
③如图4,![]() 的10 等分线相交于点
的10 等分线相交于点![]() ,若
,若![]() ,求∠A的度数.
,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是伟大的数学家欧拉亲自编的一道题:父亲临终时立下遗嘱,按下述方式分配遗产,老大分得100克朗和剩下的十分之一,老二分得200克朗和剩下的十分之一,老三分得300克朗和剩下的十分之一,老四分得400克朗和剩下的十分之一,… …,依次类推分给其余的孩子,最后发现遗产全部分完后所有孩子分得的遗产相等,遗产总数、孩子人数和每个孩子分得的遗产各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
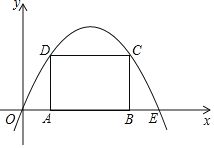
【题目】如图,抛物线y=ax2+bx(a≠0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.
(1)求抛物线的函数表达式.
(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?
(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是定长线段
是定长线段![]() 上一点,
上一点,![]() 、
、![]() 两点分别从点
两点分别从点![]() 、
、![]() 出发以1厘米/秒,2厘米/秒的速度沿直线
出发以1厘米/秒,2厘米/秒的速度沿直线![]() 向左运动(点
向左运动(点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上).
上).
(1)若点![]() 、
、![]() 运动到任一时刻时,总有
运动到任一时刻时,总有![]() ,请说明点
,请说明点![]() 在线段
在线段![]() 上的位置;
上的位置;
(2)在(1)的条件下,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值;
的值;
(3)在(1)的条件下,若点![]() 、
、![]() 运动5秒后,恰好有
运动5秒后,恰好有![]() ,此时点
,此时点![]() 停止运动,点
停止运动,点![]() 继续运动(点
继续运动(点![]() 在线段
在线段![]() 上),点
上),点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,下列结论:①
的中点,下列结论:①![]() 的值不变;②
的值不变;②![]() 的值不变.可以说明,只有一个结论是正确的,请你找出正确的结论并求值.
的值不变.可以说明,只有一个结论是正确的,请你找出正确的结论并求值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
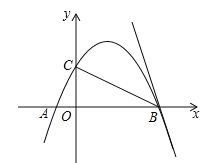
【题目】(2017广东省深圳市)如图,抛物线![]() 经过点A(﹣1,0),B(4,0),交y轴于点C;
经过点A(﹣1,0),B(4,0),交y轴于点C;
(1)求抛物线的解析式(用一般式表示);
(2)点D为y轴右侧抛物线上一点,是否存在点D使![]() ?若存在请直接给出点D坐标;若不存在,请说明理由;
?若存在请直接给出点D坐标;若不存在,请说明理由;
(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.

(1)若抛物线过点C、A、A′,求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△OC′D的周长;
(3)点M是第一象限内抛物线上的一动点,问:点M在何处时;△AMA′的面积最大?最大面积是多少?并求出此时点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com