
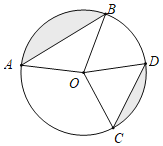
【题目】如图,已知⊙O的半径为5,弦AB=8,CD=6,则图中阴影部分面积为( )
A. ![]() π–24 B. 9π C.
π–24 B. 9π C. ![]() π–12 D. 9π–6
π–12 D. 9π–6
【答案】A
【解析】
过点O作OE⊥AB于E,作OF⊥CD于F,根据垂径定理求出AE、CF,再利用勾股定理列式求出OE=OF,从而得到AE=OF,OE=CF,然后利用“边角边”证明△AOE和△OCF全等,根据全等三角形对应角相等可得∠AOE=∠OCF,再求出∠AOE+∠COF=90°,然后求出∠AOB+∠COD=180°,把弧CD旋转到点D与点B重合,构建直角三角形ABC;然后根据圆的面积公式和直角三角形的面积公式来求阴影部分的面积:阴影面积=半圆面积-直角三角形ABC的面积.
解:如图1,过点O作OE⊥AB于E,作OF⊥CD于F,
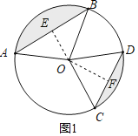
由垂径定理得,AE=![]() AB=
AB=![]() ×8=4,CF=
×8=4,CF=![]() CD=
CD=![]() ×6=3,
×6=3,
由勾股定理得,OE=![]() =
=![]() =3,
=3,
OF=![]() =
=![]() =4,
=4,
∴AE=OF,OE=CF,
在△AOE和△OCF中,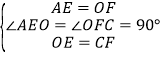 ,
,
∴△AOE≌△OCF(SAS),∴∠AOE=∠OCF,
∵∠OCF+∠COF=90°,∴∠AOE+∠COF=90°,
∴∠AOB+∠COD=2(∠AOE+∠COF)=2×90°=180°,
如图2把弧CD旋转到点D与点B重合.
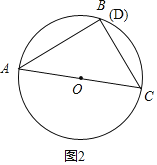
∴△ABC为直角三角形,且AC为圆的直径;
∵AB=8,CD=6,∴AC=10(勾股定理),
∴阴影部分的面积=S半圆–S△ABC=![]() π×52–
π×52–![]() ×6×8=
×6×8=![]() π–24;
π–24;
故选A.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
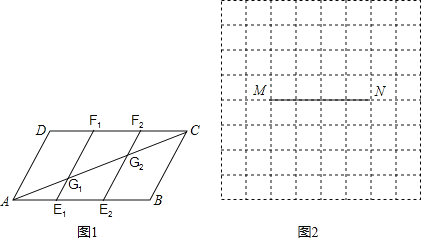
【题目】(1)如图1,在平行四边形ABCD中,点E1,E2是AB三等分点,点F1,F2是CD三等分点,E1F1,E2F2分别交AC于点G1,G2,求证:AG1=G1G2=G2C.
(2)如图2,由64个边长为1的小正方形组成的一个网格图,线段MN的两个端点在格点上,请用一把无刻度的尺子,画出线段MN三等分点P,Q.(保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
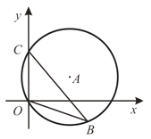
【题目】如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则∠OBC 的余弦值为 _________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,完成下列各题:
,完成下列各题:
(1)将函数关系式用配方法化为 y=a(x+h)2+k形式,并写出它的顶点坐标、对称轴.
(2)若它的图象与x轴交于A、B两点,顶点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价a元,则平均每天销售数量为 件.(用含a的代数式表示)
(2)当每件商品降价多少元时,该商店每天销售利润为1200元.
查看答案和解析>>
科目:初中数学 来源: 题型:
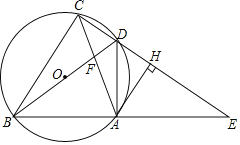
【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若![]() ,求证:CD=DH.
,求证:CD=DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
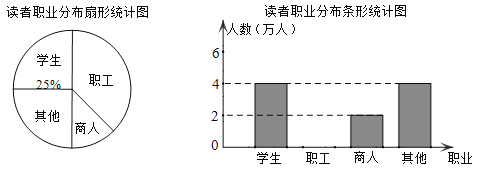
【题目】学习成为现代城市人的时尚,我市图书馆吸引了大批读者,有关部门统计了2018年第四季度到市图书馆的读者的职业分布情况,统计图如图.
(1)在统计的这段时间内,共有 万人到图书馆阅读.其中商人所占百分比是 ;
(2)将条形统计图补充完整;
(3)若今年2月到图书馆的读者共28000名,估计其中约有多少名职工.
查看答案和解析>>
科目:初中数学 来源: 题型:
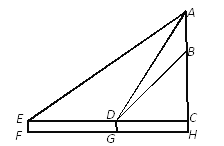
【题目】某学生为测量一棵大树AH及其树叶部分AB的高度,将测角仪放在F处测得大树顶端A的仰角为30°,放在G处测得大树顶端A的仰角为60°,树叶部分下端B的仰角为45°,已知点F、G与大树底部H共线,点F、G相距15米,测角仪高度为1.5米.求该树的高度AH和树叶部分的高度AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com