
【题目】已知AB∥CD,在AB,CD内有一条折线EGF.
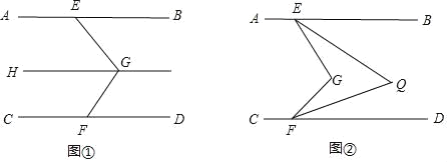
(1)如图①,过点G作GH∥AB,求证:∠BEG+∠DFG=∠EGF;
(2)如图②,已知∠BEG的平分线与∠DFG的平分线相交于点Q,请探究∠EGF与∠EQF的数量关系,并说明理由.
【答案】(1)见解析;(2)∠EQF=![]() ∠EGF,理由见解析
∠EGF,理由见解析
【解析】
(1)根据平行线的性质,两直线平行,内错角相等,即可得出∠EGH=∠BEG,∠DFG=∠FGH,即可得证;
(2)由(1)的结论得出∠EGF=∠BEG+∠DFG,∠EQF=∠BEQ+∠DFQ,然后由角平分线的性质得出∠DFQ=![]() ∠ DFG,∠BEQ=
∠ DFG,∠BEQ= ![]() ∠BEG,,进而得出∠EQF=
∠BEG,,进而得出∠EQF=![]() ∠EGF.
∠EGF.
(1)∵GH∥AB,AB∥CD,
∴GH∥CD,
∴∠EGH=∠BEG,∠DFG=∠FGH,
∵∠EGF=∠EGH+∠FGH,
∴∠BEG+∠DFG=∠EGF
(2)由(1)知,∠EGF=∠BEG+∠DFG,∠EQF=∠BEQ+∠DFQ,
∵EQ,FQ分别平分∠BEG,∠DFG,
∴∠DFQ=![]() ∠ DFG,∠BEQ=
∠ DFG,∠BEQ= ![]() ∠BEG,
∠BEG,
∴∠EQF= ![]() (∠BEG+∠DFG)=
(∠BEG+∠DFG)= ![]() ∠EGF
∠EGF


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
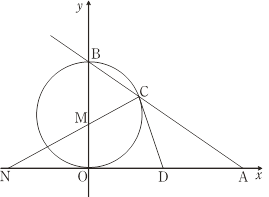
【题目】如图,已知直线AB与x轴、y轴分别交于点A和点B,OA=4,且OA,OB长是关于x的方程x2﹣mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM,交x轴于点N,点D为OA的中点.
(1)求证:CD是⊙M的切线; (2)求线段ON的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组1乘一辆汽车沿公路检修线路,约定向东为正。某天从A地出发到收工时,行走记录为(单位:千米):+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6。另一小组2也从A地出发,在南北向修,约定向北为正,行走记录为:-17,+9,-2,+8,+6,+9,-5,-1,+4,-7,-8.
(1)分别计算收工时,1,2两组在A地的哪一边,距A地多远?
(2)若每千米汽车耗油a升,求出发到收工各耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】速度分别为100km/h和akm/h(0<a<100)的两车分别从相距s千米的两地同时出发,沿同一方向匀速前行.行驶一段时间后,其中一车按原速度原路返回,直到与另一车相遇时两车停止.在此过程中,两车之间的距离y(km)与行驶时间t(h)之间的函数关系如图所示.下列说法:①a=60;②b=2;③c=b+![]() ;④若s=60,则b=
;④若s=60,则b=![]() .其中说法正确的是( )
.其中说法正确的是( )

A.①②③B.②③④C.①②④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从相距480km的A.B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
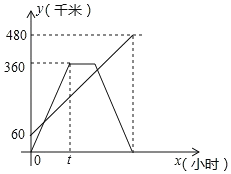
(1)乙车的速度是___千米/时,t=___小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出两车相距150千米时x的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为建设美丽农村,村委会打算在正方形地块甲和长方形地块乙上进行绿化.在两地块内分别建造一个边长为![]() 的大正方形花坛和四个边长为
的大正方形花坛和四个边长为![]() 的小正方形花坛(阴影部分),空白区域铺设草坪,记
的小正方形花坛(阴影部分),空白区域铺设草坪,记![]() 表示地块甲中空白处铺设草坪的面积,
表示地块甲中空白处铺设草坪的面积, ![]() 表示地块乙中空白处铺设草坪的面积.
表示地块乙中空白处铺设草坪的面积.

(1)![]() __ ,
__ ,![]() (用含
(用含![]() 的代数式表示并化简) .
的代数式表示并化简) .
(2)若![]() ,求
,求![]() 的值.
的值.
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,每个小正方形的边长都为1个单位长度,三角形![]() 的顶点都在正方形网格的格点上,将三角形
的顶点都在正方形网格的格点上,将三角形![]() 经过平移后得到三角形
经过平移后得到三角形![]() ,其中点
,其中点![]() 是点
是点![]() 的对应点.
的对应点.

(1)画出平移后得到的三角形![]() ;
;
(2)连接![]() 、
、![]() ,则线段
,则线段![]() 、
、![]() 的关系为______;
的关系为______;
(3)四边形![]() 的面积为______(平方单位).
的面积为______(平方单位).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com