
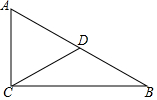
 如图,Rt△ABC中,∠ACB=90°,∠B=30°,点D为AB的中点,则∠ACD=60°.
如图,Rt△ABC中,∠ACB=90°,∠B=30°,点D为AB的中点,则∠ACD=60°.  新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 平面直角坐标系xOy中,抛物线y=mx2-2m2x+2交y轴于A点,交直线x=4于B点.
平面直角坐标系xOy中,抛物线y=mx2-2m2x+2交y轴于A点,交直线x=4于B点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
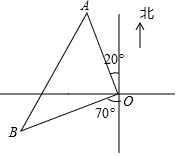 如图,一艘货轮和一艘渔船同时从港口O出发,货轮沿北偏西20°方向航行60海里到达点A处,此时,渔船到达港口O南偏西70°的点B处,与港口O相距80海里,求此时货轮和渔船之间的距离.
如图,一艘货轮和一艘渔船同时从港口O出发,货轮沿北偏西20°方向航行60海里到达点A处,此时,渔船到达港口O南偏西70°的点B处,与港口O相距80海里,求此时货轮和渔船之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 选取该校50名女生 | B. | 选取该校50名男生 | ||
| C. | 选取该校一个班级的学生 | D. | 随机选取该校50名学生 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com