
【题目】已知![]() 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点![]() 点D不与B,C重合
点D不与B,C重合![]() 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
![]() 如图1,求证:
如图1,求证:![]() ≌
≌![]() ;
;
![]() 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;
![]() 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问![]() 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.

【答案】(1)见解析;(2) 四边形BCEF是平行四边形,理由见解析;(3) 成立,理由见解析.
【解析】
(1)利用有两条边对应相等并且夹角相等的两个三角形全等即可证明△AFB≌△ADC;
(2)四边形BCEF是平行四边形,因为△AFB≌△ADC,所以可得∠ABF=∠C=60°,进而证明∠ABF=∠BAC,则可得到FB∥AC,又BC∥EF,所以四边形BCEF是平行四边形;
(3)易证AF=AD,AB=AC,∠FAD=∠BAC=60°,可得∠FAB=∠DAC,即可证明△AFB≌△ADC;根据△AFB≌△ADC可得∠ABF=∠ADC,进而求得∠AFB=∠EAF,求得BF∥AE,又BC∥EF,从而证得四边形BCEF是平行四边形.
![]() 和
和![]() 都是等边三角形,
都是等边三角形,
![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
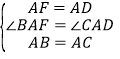 ,
,
![]() ≌
≌![]() ;
;
![]() 由
由![]() 得
得![]() ≌
≌![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() 四边形BCEF是平行四边形;
四边形BCEF是平行四边形;
![]() 成立,理由如下:
成立,理由如下:
![]() 和
和![]() 都是等边三角形,
都是等边三角形,
![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
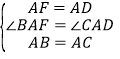 ,
,
![]() ≌
≌![]() ;
;
![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() 四边形BCEF是平行四边形.
四边形BCEF是平行四边形.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx与直线y=2x+4交于A(a,8)、B两点,点P是抛物线上A、B之间的一个动点,过点P分别作x轴、y轴的平行线与直线AB交于点C和点E.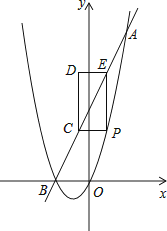
(1)求抛物线的解析式;
(2)若C为AB中点,求PC的长;
(3)如图,以PC,PE为边构造矩形PCDE,设点D的坐标为(m,n),请求出m,n之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.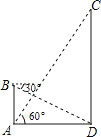
(1)求教学楼与旗杆的水平距离AD;(结果保留根号)
(2)求旗杆CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+b的图象与反比例函数y= ![]() (k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
(k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1). 
(1)求反比例函数的表达式和a、b的值;
(2)若A、O两点关于直线l对称,请连接AO,并求出直线l与线段AO的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,CE是△ABC的角平分线.
(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( ) 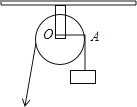
A.πcm
B.2πcm
C.3πcm
D.5πcm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠CAD.
(1)求证:直线MN是⊙O的切线;
(2)若CD=3,∠CAD=30°,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com