
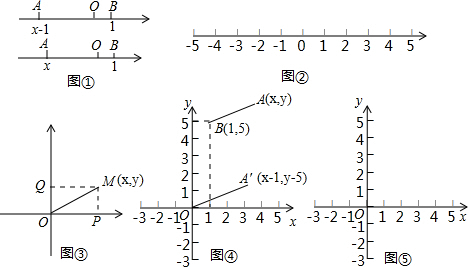
分析 探究一(3)由于|x-1|表示数轴上x所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点对应的数x的范围,从而画出数轴即可.
探究二(3)由于$\sqrt{(x+3)^{2}+(y-4)^{2}}$的几何意义是:点A(x,y)与B(-3,4)之间的距离,所以构造直角三角形利用勾股定理即可得出答案.
(4)根据前面的探究可知$\sqrt{(x-a)^{2}+(y-b)^{2}}$的几何意义是表示点(x,y)与点(a,b)之间的距离;
拓展应用
(1)根据探究二(4)可知点F的坐标;
(2)根据三角形的三边关系即可求出答案.
解答 解:探究一:(3)如图所示,
∴| x-1|<2的解集是-1<x<3,
x-1|<2的解集是-1<x<3,
探究二:(3)如图⑤,在直角坐标系中,设点A′的坐标为(x+3,y-4),由探究二(1)可知,A′O=$\sqrt{(x+3)^{2}+(y-4)^{2}}$,将线段A′O先向左平移3个单位,再向上平移4个单位,得到线段AB,此时点A的坐标为(x,y),点B的坐标为(-3,4),因为AB=A′O,所以AB=$\sqrt{(x+3)^{2}+(y-4)^{2}}$,因此$\sqrt{(x+3)^{2}+(y-4)^{2}}$的几何意义可以理解为点A(x,y)与点B(-3,4)之间的距离AB.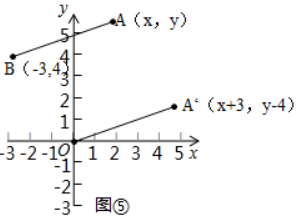
(4)根据前面的探究可知$\sqrt{(x-a)^{2}+(y-b)^{2}}$的几何意义是表示点(x,y)与点(a,b)之间的距离;
拓展应用:(1)由探究二(4)可知$\sqrt{(x+1)^{2}+(y+5)^{2}}$表示点(x,y)与(-1,-5)之间的距离,
故F(-1,-5),
(2)由(1)可知:$\sqrt{(x-2)^{2}+(y+1)^{2}}$+$\sqrt{(x+1)^{2}+(y+5)^{2}}$表示点A(x,y)与点E(2,-1)的距离和点A(x,y)与点F(-1,-5)的距离之和,
当A(x,y)位于直线EF外时,
此时点A、E、F三点组成△AEF,
∴由三角形三边关系可知:EF<AF+AE,
当点A位置线段EF之间时,此时EF=AF+AE,
∴$\sqrt{(x-2)^{2}+(y+1)^{2}}$+$\sqrt{(x+1)^{2}+(y+5)^{2}}$的最小值为EF的距离,
∴EF=$\sqrt{(2+1)^{2}+(-1+5)^{2}}$=5
故答案为:探究二(4)点(x,y)与点(a,b)之间的距离;
拓展应用(1)(-1,-5);(2)5.
点评 本题考查学生的阅读理解能力,解题的关键是正确理解题意,仿照题意求出答案,本题考查学生综合能力,属于中等题型.


科目:初中数学 来源: 题型:填空题
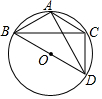 如图,等腰△ABC内接于⊙O,已知AB=AC,∠ABC=30°,BD是⊙O的直径,如果CD=$\frac{4\sqrt{3}}{3}$,则AD=4.
如图,等腰△ABC内接于⊙O,已知AB=AC,∠ABC=30°,BD是⊙O的直径,如果CD=$\frac{4\sqrt{3}}{3}$,则AD=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
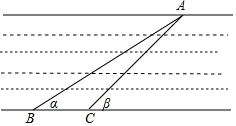 如图,为了测量某条河的宽度,现在河边的一岸边任意取一点A,又在河的另一岸边去两点B、C测得∠α=30°,∠β=45°,量得BC长为100米.求河的宽度(结果保留根号).
如图,为了测量某条河的宽度,现在河边的一岸边任意取一点A,又在河的另一岸边去两点B、C测得∠α=30°,∠β=45°,量得BC长为100米.求河的宽度(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
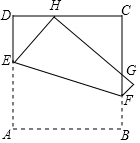 如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD的周长为m,△CHG的周长为n,则$\frac{n}{m}$的值为( )
如图,将正方形ABCD折叠,使顶点A与CD边上的一点H重合(H不与端点C,D重合),折痕交AD于点E,交BC于点F,边AB折叠后与边BC交于点G.设正方形ABCD的周长为m,△CHG的周长为n,则$\frac{n}{m}$的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | ||
| C. | $\frac{\sqrt{5}-1}{2}$ | D. | 随H点位置的变化而变化 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com